Team:NTNU Trondheim/Journal Modeling
From 2011.igem.org

Journal for Modeling Group
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
You can find an overview of the modeling here.
Wednesday 22/6
Introductory lectures in systems biology was held by Marius Eidsaa. Different approaches were discussed and it was decided to work with two different models: Bayesian Networks and systems of Ordinary Differential Equations, and possibly extend it to Stochastic Differential Equations.
Friday 24/6
Dizzy was installed and we started to look at how to simulate Michealis Menten reactions.
Monday 27/6
We continued where we ended last week, with having lectures and to get aquinted with different software.
Thursday 30/6
A program which solves ordinary differential equations numerically using the Runge Kutta method of order 4 and 5 was made in Matlab. Using equation (*) and (**) (see the ) and having the level of ppGpp fixed the reponse of the system could be found.
The Bayesian model started to take form, and is ready to be implemented in C++.
Friday 1/7
The program was tested to see if it gave reasonable results. Minor errors were corrected and the first results were obtained, due to a lack of accurate parameters the units on the axis are arbitrary. Here is the Matlab code:
tspan=[0;20]; % defines the start and stop
x=10.0; %the initial conentration of ppGpp
%the initial concentrations of LacI mRNA, LacI, mCherry mRNA and mCherry
y0=[20;20;0;0];
[T Y]=ode45(@F,tspan,y0);
plot(T,Y(:,2),T,Y(:,4),'r')
ppGpp=num2str(x);
title(['ppGpp=',ppGpp])
legend('LacI','mCherry','Location','East')
xlabel('t(a.u)')
ylabel('Concentration (a.u)')
Where F is a function defined by:
function Y = F(t,y)
Y=zeros(4,1);
x=10.0;
k1=[5e-4;5e-4];
k_prime=[20.0;20.0];
d1=[1;1];
n=[1;1];
k2=[20;20];
d2=[20;20];
Y(1)=k1(1)+k_prime(1)/(1+(y(5)+x)^n(1))-d1(1)*y(1);
Y(2)=k2(1)*y(1)-d2(1)*y(2);
Y(3)=k1(2)+k_prime(2)/(1+y(2)^n(2))-d1(2)*y(3);
Y(4)=k2(2)*y(3)-d2(2)*y(4);
end
The resulting plot is shown in this figure.
Monday 4/7
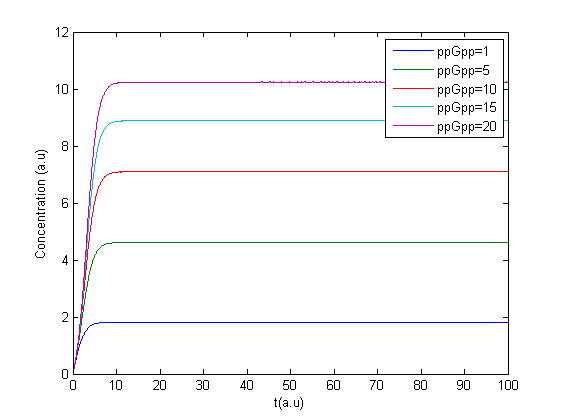
The program was modified to make it possible to have several values of ppGpp in one run making it possible to see the response to different values of ppGpp, see figure.
The theory for the Bayesian model seems to be in place, see figure , some of the implementation has already been done in C++.Thursday 7/7
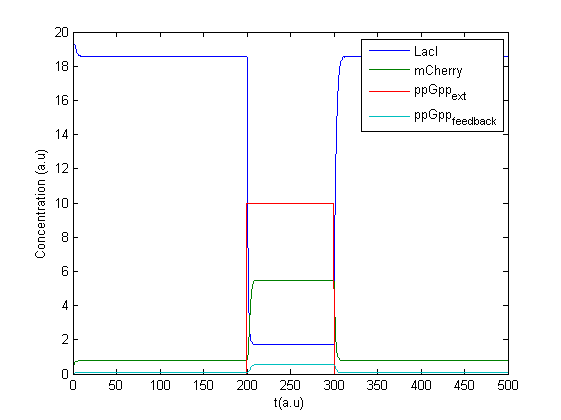
A new program was made in Matlab to treat the concentration of ppGpp as an input signal. A possible feedback effect was also included as production of mCherry might lead to increase in ppGpp. The concentration of ppGpp was split into two parts, one external controlled and one caused by feedback , see figure.
Friday 8/7
We was given an introductory lecture in Biology and Biotechnology by Gunnvor , to get an understanding of the work beeing done at the lab.
Monday 11/7
After a team meeting we was given a Master Thesis by Sigurd Johansen describing a toogle switch. We started to expand the ODE model to include more reactions than we have done so far. Both to be aware of possible limitations of the current model and to get a clearer understanding of the fundamental processes involved.
Started to investigate how to model and solve stochastic differential equations, and how to derive them from physical properties.
Thursday 14/7
We contacted the lab group to clarify the way ppGpp inhibits the rrnB promotor and was informed that it affects the RNAp and not the promotor in itself and can therefore also affect pLac.
The theory behind stochastic differential equation was investigated further.
Wednesday 20/7
We contacted Autodesk to explore the possibility of using Maya and the mMaya toolkit to visiualize the system. We also visited the lab to see how gelelectrophoresis was performed.
Thursday 21/7
We recieved mail from Autodesk, installed mMaya and explored the possibility of creating animations.
Friday 22/7
A simple animation of a green bacteria (or something resembling that) turning red was made in Maya.
Wednesday 27/7
Meeting with prof. Almaas.
We decided to drop the bayesian model see here, and focus on stochastic models.
Thursday 28/7
Dizzi was installed on one of the calculations server at NTNU, Dept. of Mathematics.
An electronic mail was send to see if another iGEM team needed help (requirement for gold medal).
 "
"