Team:KAIST-Korea/Projects/Modeling/Section2

Quorum Diffusion

E.casso uses the communication between cells made available by quorum sensing. Quorum diffuses away from one cell to the other. Because we wanted to find out how the quorums produced by Brush E.coli diffuse in our model, we applied the reaction-diffusion system to our model and analyzed the distribution and propagation of quorums. This section investigates how the quorums diffuse from one cell to the other which will provide crucial data for our final simulation. The main purposes of this modeling is to answer the following questions:

1. How fast does quorum diffuse into adjacent E. coli as rapidly as we predicted?
2. How does the produced quorum diffuse with respect to time and space?
3. How much quorum does the source E. coli ultimately transfer to neighboring E. coli?

Modeling Approach

Fig 1. (a) Approximation of the dimensions of E.coli as a square having equal area (b) Schematic representation of E.coli distribution model on a grid

According to the statistics on E. coli^[1], the shape of E.coli is oval with 200nm minor axis and 2um major axis. For simulating our random diffusion system in E.casso, we simply the E.coli shape as square having equal area with the area of oval. (Fig 1a)

where d is the side length of the square

Based on this calculation, we can assume a two dimensional distribution model in which E.colis are distributed on a grid that consists of squares of side 1.1 micrometer. (Fig 1b) In each square, there may exist a brush E.coli, a paint E.coli, or nothing.

According to the statistics on E. coli^[1], the speed of a small molecule in the cytoplasm is 50 nanometers per millisecond. Also, all molecules move by random walk during diffusion.^[2] Using Python, we ran a simulation on the random walk of a quorum molecule. It was assumed that each step takes 0.2 milliseconds.

Fig 2. A two-dimensional random walk of a quorum molecule simulated using python language. The simulation was repeated a hundred times.

For each trial, we measured the time it took the molecule to go out of bounds. Averaging the time for a hundred trials yielded that a quorum molecule takes about 449 milliseconds to diffuse to an adjacent cell. (Fig 2) In other words, it takes about 0.45 seconds for a quorum molecule produced in one cell to diffuse into the center of a nearby cell. Since this is much smaller than the minute time-scale considered in our following analysis, we can ignore the diffusion speed.

Our quorum diffusion system follows a mathematical description of the change in concentration of one or more substances in space as a result of diffusion or chemical reaction.

where q(x, t) is the distribution of the number of a substance as a function of time and distance from a reference point, D is a diagonal matrix of Diffusion coefficients, and R is an equation of local reaction.

In regard to quorum, the equation can be written as,

where R(q) stands for the diffusion reaction. By Fick's second law^[4],

The final equation becomes^[5],

where diffusion coefficient of Autoinducer ^[6]

Initially, the concentration of quorum is zero. Hence, q(x,0) is zero. The boundaries conditions are that the rate of production of quorum is constant and that the concentration approaches zero as distance increases. From the previous results, we obtain that 40 quorums are produced per minute.

Results & Conclusion

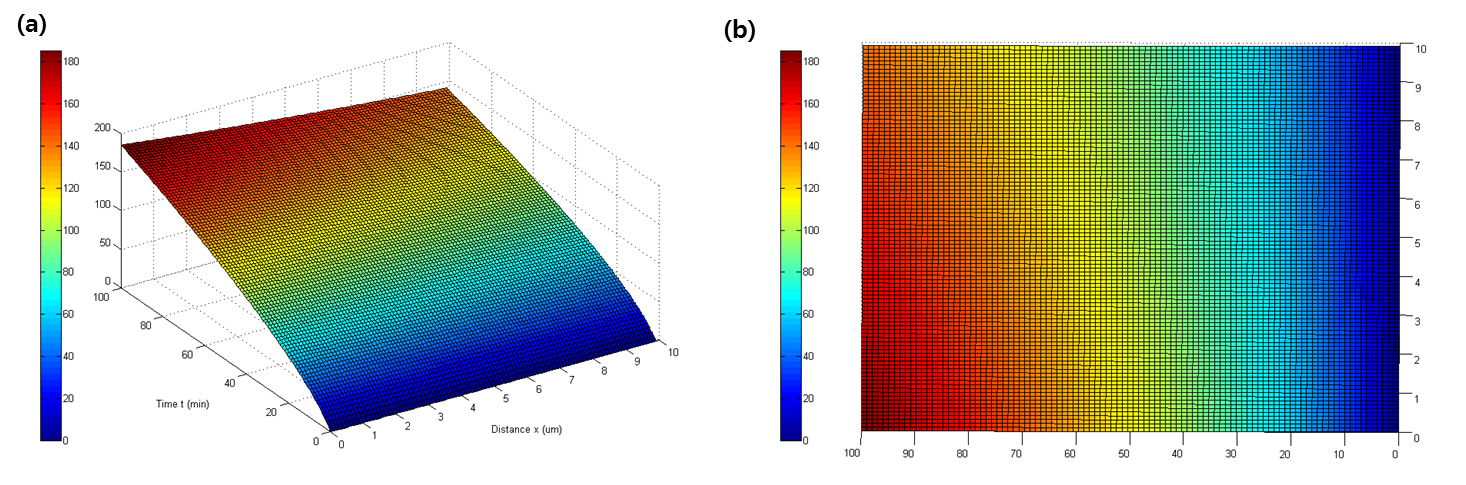
Using the pdepe function which indicates partial differential equation in MATLAB and considering E. coli as a point in space, the following graph represents the concentration as a function of time and distance.

Fig 3. Quorum Diffusion from E.coli1 computed with 100 mesh points in (a) three and (b) two dimensions.

As expected, q decreases as distance increases, and increases as time progresses. (Fig. 3)

In the distribution model, the distinct between two horizontal and two vertical adjacent cells are 1.1um, and the distinct between four adjacent diagonal cells is1.56 um.(Fig 1) Therefore, the average distinct between any two adjacent cells is 1.33um. Essentially, q(1.3 um, t) tells us the concentration of quorum that diffuses from an E. coli to an adjacent cell as a function of time.

If we plot this using MATLAB, we can represent as in the following graph the concentration of quorum that diffuses to an adjacent cell as a function of time.

Fig 4. The quorum concentration at a distance x away from E.coli as a function of time during the first (a) 10min and (b)<100min.

As time goes on, E. coli produces more and more quorum, which diffuses to adjacent E. coli. (Fig 4) Although theory predicts forty quorum molecules are produced per minute, the actual number of quorum molecules present at the site of production (at x = 0) is only around two to three because they diffuse away very rapidly. Although the concentration of quorum tend to be lower at 1.3 um from the site of production, the concentration in both the origin and the destination reaches about 180 molecules as time passes 100 minutes.

How much quorum does adjacent E. coli receive? In reality, E. coli are not point particles in space. In order to predict the actual amount of quorum in E. coli, it is necessary to integrate q from distance 0 to 0.5 um. For simplicity, we simply add quorums at distances from 0 until 0.5 um at an interval of 0.1 um. To calculate the total amount of quorum dispersed to adjacent cells, we add quorum concentrations from 0.6 to 1.6 um at the same interval of 0.1 um. Because we assume a two dimensional tightly on previous analysis, we simply divide the result by 8 to obtain the amount of quorum that one cell receives.

Fig 5. Total quorum contained within distinct boundaries

After 100 minutes, 920 quorums will be left in the source E. coli, and 2000 quorums will have been dispersed to all adjacent E. coli. (Fig 5) In conclusion, each adjacent E. coli receives one fourth the quorum contained within the source E. coli.

References

[1] "E. Coli Statistics." CCDB. Web. 15 July 2011. <http://www.ccdb.ualberta.ca/CCDB/cgi-bin/STAT_NEW.cgi>.

[2] Howard C. Berg, Random Walks in biology, Princeton Paperbacks, New expanded edition (1993)

[3] A. Kolmogorov et al., Moscow Univ. Bull. Math. A 1 (1937): 1

[4] R. A. Fisher, Ann. Eug. 7 (1937): 355

[5] P. C. Fife, Mathematical Aspects of Reacting and Diffusing Systems, Springer (1979)

[6] Mark R. Tinsley, Annette F. Taylor, Zhaoyang Huang, and Kenneth Showalter, Emergence of Collective Behavior in Groups of Excitable Catalyst-Loaded Particles: Spatiotemporal Dynamical Quorum Sensing, Physical Review Letters, 102, 158301 (2009)