Team:KAIST-Korea/Projects/report 12
From 2011.igem.org
(Created page with "{{:Team:KAIST-Korea/jihan}} __NOTOC__ <html> <head> <style type="text/css"> #TagHome{ position: absolute; font-family:Bell MT; font-size:12pt; le...") |
|||
| Line 38: | Line 38: | ||
<div id="kaistcontent"> | <div id="kaistcontent"> | ||
| - | =='''Quorum | + | =='''Quorum Production by the Brush E. coli'''== |
| - | + | Mathematical modeling is essential in qualitatively describing de novo genetic circuits that frequently arise in synthetic biology. We can use such models for two objectives: (1) predicting the behavior of combinations of BioBrick parts designed for the synthetic circuit that performs some task, and (2) choosing the appropriate promoter and ribosome binding site (RBS) with suitable strengths for the circuit. Also, it will serve as a reference for others who use the BioBrick in the future. In summary, the model and the computer simulation are our beginning point for making testable predictions about the behavior of our system. We construct a computational model describing the genetic network encompassing relevant signal transduction pathways in order to help build E.coli that can draw pictures! | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | ===Modeling | + | ===Modeling E.coli Type I. (Brush E.coli)=== |
---- | ---- | ||
| + | ===='''Modeling Approach'''==== | ||
| + | |||
| + | :There are several known Quorum sensing (QS) networks. All known QS networks operate as an “on-off” gene expression switch by controlling the level of a certain transcription factor whose expression is suppressed in the “off” state and is strongly induced in the “on” state.[2] Usually, the intracellular network that is controlled by the quorum sensing remains in the “off” state until the quorum reaches a certain concentration. After quorum reaches the threshold concentration, the genetic circuit changes its state into “on” state and activates the expression of the relevant genes. In this model, we hypothesized that the typical E.coli cell volume is ~7.0×10-16L and cells are freely permeable to quorums. We used a standard chemical kinetic approach based on the mass-action rate law. The kinetic parameters used in our model are based on the published data. The rate constants were taken from several papers on the mathematical modeling of quorum sensing pathways. | ||
| + | |||
| + | ===='''Model'''==== | ||
| + | :Before moving on to our model system, let us review how to model a general case of protein production from a single gene. | ||
| + | |||
| + | ====='''Protein Production of a Single Gene Modeling'''===== | ||
| + | |||
| + | :The actual protein production from a single gene is composed of complex processes. However, in this model, protein production is simplified into two processes: transcription and translation. | ||
| + | |||
| + | [[File:Ecasso-report1-figure01.jpg|800px|thumb|center| Fig 1.The schematic diagram of protein production modeling | ||
| + | The model can be represented by these chemical reactions with corresponding ordinary differential equations (ODEs):]] | ||
| + | |||
| + | :where pm is the mRNA production rate constant, and pp is the protein production rate constant. Although the choice of parameters depends on many factors such as the gene of interest and the internal and external environment of gene expression, the commonly accepted estimation of parameters is sufficient for our gene expression model. Therefore, we choose the average transcription/translation rate constants which are taken from published data. [1] | ||
| + | |||
| + | :The degradation rate of the mRNA and protein can be calculated from | ||
| + | |||
| + | :where t1/2is the degradation half-life in minutes. From this equation, we can calculate kmd(mRNA degradation rate), kpd(protein degradation rate). The values are in the constants table. [3. Constants Table of this page] Based on these facts and the law of mass action, we can write these equations: | ||
| + | |||
| + | :The above models an average protein production from a single gene. However, in synthetic biology, we can control the transcription rate and the translation rate by appropriately changing the promoter and RBS parts. Therefore, we can represent the rate constants differently: | ||
| + | |||
| + | :where χp is the strength ratio of the promoter relative to the average rate of transcription. Also, χR is the strength ratio of RBS relative to the average rate of translation. It is determined by the promoter (or RBS) BioBrick part that we use. | ||
| + | |||
| + | :We will refer to the aforementioned protein production rate of a single gene model to build our own models. If specific values for the production and degradation rates exist for a certain protein, we will use those values. Otherwise, we will use a general, averaged value like above model. Let’s jump right into the details of the model. | ||
| + | |||
| + | ====='''Modeling of Brush (Type II) E.coli'''===== | ||
| + | |||
| + | [[File:Ecasso-report1-figure02.jpg|800px|thumb|center| Fig 2. The schematic diagram of Brush E.coli modeling.]] | ||
| + | |||
| + | :The above schematic diagram represents the genetic circuit implmented in the Brush E.coli after it has been genetically recombined by the Cre-Lox system[HYPERLINK TO THE WIKIPEDIA]. The Cre-Lox recombination system is commonly used to knockout a specific gene conditionally, in which a gene is only knocked out at a specific time. By using this Cre-Lox recombination system, one of the four quorum sensing systems is chosen and installed in Brush E.coli (In this model, the Lux based quorum sensing system is installed). In our model, we will only discuss the system embedded with the Lux system and assume that the model is applicable to the other three installations because they operate with an almost identical mechanism and have similar reaction constants. Now, we briefly explain each component of the model in the following paragraphs. | ||
| + | |||
| + | #DNA1 translates LacI constituitively. As a derivative of the lac operon, LacI binds to the gene lacO to suppress the expression of the genes downstream relative to lacO. Although four LacI must bind to lacO for this to occur, we assume one is sufficient so that we can simplify the analysis. | ||
| + | |||
| + | #DNA2 produces LuxI, the component of the Lux based quorum sensing. LacI suppresses expression of DNA2 by binding to the LacO which is upstream to the luxI gene. As a result, DNA2 is not translated until we add IPTG. | ||
| + | |||
| + | #When we add IPTG, it binds with LacI. IPTG acts as a competitive inhibitor to the binding of LacI to lacO; IPTG prevents LacI from binding to DNA2, clearing way for the RNA Polymerase to begin transcription. That is, IPTG induces the translation of luxI in DNA2; it is an inducing signal that turns the switch on.[2] In this model, we assumed that IPTG is applied in the form of a step function. | ||
| + | |||
| + | :In order to describe the behaviour of the circuit with a deterministic model, we used the mass action rate laws in part A to represent changes of each quantity with respect to time in a set of ordinary differential equations. By solving these equations, we can obtain the number of each variable at a specific time. (Note, we used the Michaelis-Menten equation to account for the affinity difference of LacI for both for LacO and IPTG. Detailed explanation will follow.) | ||
| + | |||
| + | <center>* Refer to the constants table for the constants</center> | ||
| + | The brackets represent the number of molecules of the species enclosed between them. For instance, [LacI]T indicates the number of LacI in the cell, [LacIFree] the number of LacI molecules not bound to an IPTG. The equation for [LacIFree] was derived from the Michaelis-Menten equation. For the derivation, refer to page 241-245 of the reference [11]. | ||
| + | |||
| + | |||
| + | Because of the proportion of LacI molecules that form a complex with IPTG, only [LacIFree] LacI molecules can bind to DNA2. When there are the same number of repressor molecules, the promoter activity is given by the following equation, derived from the equation for the chemical equilibrium. | ||
| + | |||
| + | |||
| + | |||
| + | where k5 is the transcription rate of DNA2 (refer to page 248-250 of the reference [11] for details). Using this equation, we can obtain the rate equations for mRNA2 and LuxI. | ||
| + | |||
| + | |||
| + | |||
| + | By solving these ordinary equations, we can model the response of the genetically engineered E.coli to IPTG and also obtain the number of LuxI in the cell. Using the latter we now find out the number of quorum molecules produced by Brush E.coli per unit time, as well as the amount diffused to nearby cells. | ||
| - | |||
| - | |||
| - | |||
| - | |||
:According to the statistics on E. coli<sup>[1]</sup>, the speed of a small molecule in the cytoplasm is 50 nanometers per millisecond. Also, all molecules move by random walk during diffusion.<sup>[2]</sup> Using Python, we ran a simulation on the random walk of a quorum molecule. It was assumed that each step takes 0.2 milliseconds. | :According to the statistics on E. coli<sup>[1]</sup>, the speed of a small molecule in the cytoplasm is 50 nanometers per millisecond. Also, all molecules move by random walk during diffusion.<sup>[2]</sup> Using Python, we ran a simulation on the random walk of a quorum molecule. It was assumed that each step takes 0.2 milliseconds. | ||
Revision as of 09:26, 7 August 2011
Quorum Production by the Brush E. coli
Mathematical modeling is essential in qualitatively describing de novo genetic circuits that frequently arise in synthetic biology. We can use such models for two objectives: (1) predicting the behavior of combinations of BioBrick parts designed for the synthetic circuit that performs some task, and (2) choosing the appropriate promoter and ribosome binding site (RBS) with suitable strengths for the circuit. Also, it will serve as a reference for others who use the BioBrick in the future. In summary, the model and the computer simulation are our beginning point for making testable predictions about the behavior of our system. We construct a computational model describing the genetic network encompassing relevant signal transduction pathways in order to help build E.coli that can draw pictures!
Modeling E.coli Type I. (Brush E.coli)
Modeling Approach
- There are several known Quorum sensing (QS) networks. All known QS networks operate as an “on-off” gene expression switch by controlling the level of a certain transcription factor whose expression is suppressed in the “off” state and is strongly induced in the “on” state.[2] Usually, the intracellular network that is controlled by the quorum sensing remains in the “off” state until the quorum reaches a certain concentration. After quorum reaches the threshold concentration, the genetic circuit changes its state into “on” state and activates the expression of the relevant genes. In this model, we hypothesized that the typical E.coli cell volume is ~7.0×10-16L and cells are freely permeable to quorums. We used a standard chemical kinetic approach based on the mass-action rate law. The kinetic parameters used in our model are based on the published data. The rate constants were taken from several papers on the mathematical modeling of quorum sensing pathways.
Model
- Before moving on to our model system, let us review how to model a general case of protein production from a single gene.
Protein Production of a Single Gene Modeling
- The actual protein production from a single gene is composed of complex processes. However, in this model, protein production is simplified into two processes: transcription and translation.
- where pm is the mRNA production rate constant, and pp is the protein production rate constant. Although the choice of parameters depends on many factors such as the gene of interest and the internal and external environment of gene expression, the commonly accepted estimation of parameters is sufficient for our gene expression model. Therefore, we choose the average transcription/translation rate constants which are taken from published data. [1]
- The degradation rate of the mRNA and protein can be calculated from
- where t1/2is the degradation half-life in minutes. From this equation, we can calculate kmd(mRNA degradation rate), kpd(protein degradation rate). The values are in the constants table. [3. Constants Table of this page] Based on these facts and the law of mass action, we can write these equations:
- The above models an average protein production from a single gene. However, in synthetic biology, we can control the transcription rate and the translation rate by appropriately changing the promoter and RBS parts. Therefore, we can represent the rate constants differently:
- where χp is the strength ratio of the promoter relative to the average rate of transcription. Also, χR is the strength ratio of RBS relative to the average rate of translation. It is determined by the promoter (or RBS) BioBrick part that we use.
- We will refer to the aforementioned protein production rate of a single gene model to build our own models. If specific values for the production and degradation rates exist for a certain protein, we will use those values. Otherwise, we will use a general, averaged value like above model. Let’s jump right into the details of the model.
Modeling of Brush (Type II) E.coli
- The above schematic diagram represents the genetic circuit implmented in the Brush E.coli after it has been genetically recombined by the Cre-Lox system[HYPERLINK TO THE WIKIPEDIA]. The Cre-Lox recombination system is commonly used to knockout a specific gene conditionally, in which a gene is only knocked out at a specific time. By using this Cre-Lox recombination system, one of the four quorum sensing systems is chosen and installed in Brush E.coli (In this model, the Lux based quorum sensing system is installed). In our model, we will only discuss the system embedded with the Lux system and assume that the model is applicable to the other three installations because they operate with an almost identical mechanism and have similar reaction constants. Now, we briefly explain each component of the model in the following paragraphs.
- DNA1 translates LacI constituitively. As a derivative of the lac operon, LacI binds to the gene lacO to suppress the expression of the genes downstream relative to lacO. Although four LacI must bind to lacO for this to occur, we assume one is sufficient so that we can simplify the analysis.
- DNA2 produces LuxI, the component of the Lux based quorum sensing. LacI suppresses expression of DNA2 by binding to the LacO which is upstream to the luxI gene. As a result, DNA2 is not translated until we add IPTG.
- When we add IPTG, it binds with LacI. IPTG acts as a competitive inhibitor to the binding of LacI to lacO; IPTG prevents LacI from binding to DNA2, clearing way for the RNA Polymerase to begin transcription. That is, IPTG induces the translation of luxI in DNA2; it is an inducing signal that turns the switch on.[2] In this model, we assumed that IPTG is applied in the form of a step function.
- In order to describe the behaviour of the circuit with a deterministic model, we used the mass action rate laws in part A to represent changes of each quantity with respect to time in a set of ordinary differential equations. By solving these equations, we can obtain the number of each variable at a specific time. (Note, we used the Michaelis-Menten equation to account for the affinity difference of LacI for both for LacO and IPTG. Detailed explanation will follow.)
The brackets represent the number of molecules of the species enclosed between them. For instance, [LacI]T indicates the number of LacI in the cell, [LacIFree] the number of LacI molecules not bound to an IPTG. The equation for [LacIFree] was derived from the Michaelis-Menten equation. For the derivation, refer to page 241-245 of the reference [11].
Because of the proportion of LacI molecules that form a complex with IPTG, only [LacIFree] LacI molecules can bind to DNA2. When there are the same number of repressor molecules, the promoter activity is given by the following equation, derived from the equation for the chemical equilibrium.
where k5 is the transcription rate of DNA2 (refer to page 248-250 of the reference [11] for details). Using this equation, we can obtain the rate equations for mRNA2 and LuxI.
By solving these ordinary equations, we can model the response of the genetically engineered E.coli to IPTG and also obtain the number of LuxI in the cell. Using the latter we now find out the number of quorum molecules produced by Brush E.coli per unit time, as well as the amount diffused to nearby cells.
- According to the statistics on E. coli[1], the speed of a small molecule in the cytoplasm is 50 nanometers per millisecond. Also, all molecules move by random walk during diffusion.[2] Using Python, we ran a simulation on the random walk of a quorum molecule. It was assumed that each step takes 0.2 milliseconds.
- For each trial, we measured the time it took the molecule to go out of bounds. Averaging the time for a hundred trials yielded that a quorum molecule takes about 449 milliseconds to diffuse to an adjacent cell. (Fig 2) In other words, it takes about 0.45 seconds for a quorum molecule produced in one cell to diffuse into the center of a nearby cell. Since this is much smaller than the minute time-scale considered in our following analysis, we can ignore the diffusion speed.
- Our quorum diffusion system follows a mathematical description of the change in concentration of one or more substances in space as a result of diffusion or chemical reaction.
- where q(x, t) is the distribution of the number of a substance as a function of time and distance from a reference point, D is a diagonal matrix of Diffusion coefficients, and R is an equation of local reaction.
- In regard to quorum, the equation can be written as,
- where R(q) stands for the diffusion reaction. By Fick's second law[4],
- The final equation becomes[5],
- where diffusion coefficient of Autoinducer [6]
- Initially, the concentration of quorum is zero. Hence, q(x,0) is zero. The boundaries conditions are that the rate of production of quorum is constant and that the concentration approaches zero as distance increases. From the previous results, we obtain that 40 quorums are produced per minute.
Results & Conclusion
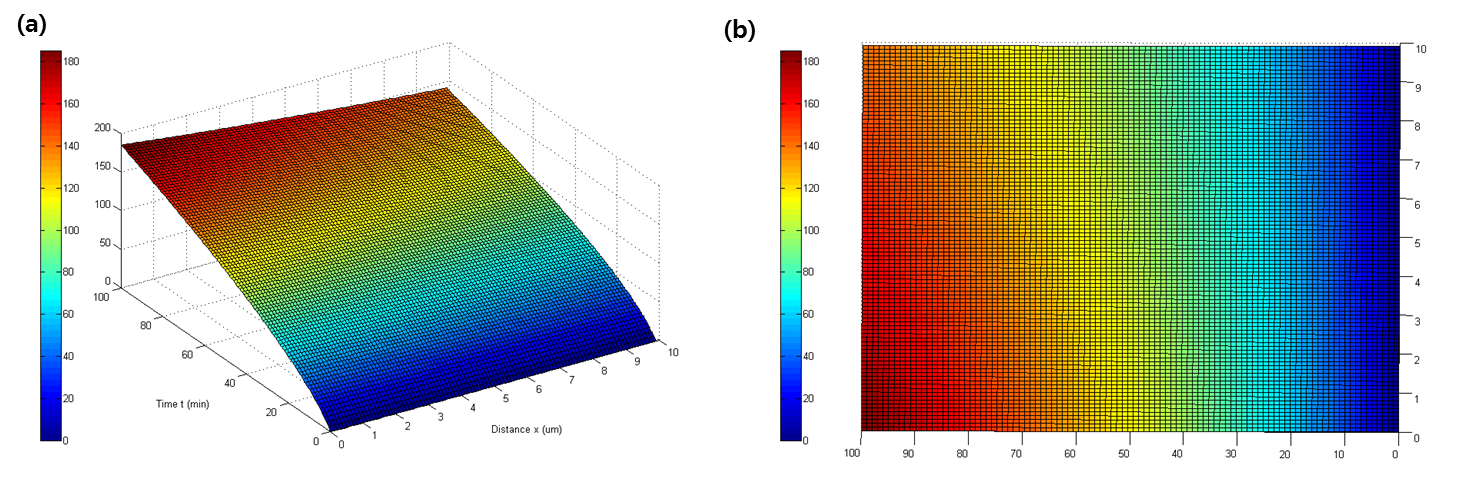
- Using the pdepe function which indicates partial differential equation in MATLAB and considering E. coli as a point in space, the following graph represents the concentration as a function of time and distance.
- As expected, q decreases as distance increases, and increases as time progresses. (Fig. 3)
- In the distribution model, the distinct between two horizontal and two vertical adjacent cells are 1.1um, and the distinct between four adjacent diagonal cells is1.56 um.(Fig 1) Therefore, the average distinct between any two adjacent cells is 1.33um. Essentially, q(1.3 um, t) tells us the concentration of quorum that diffuses from an E. coli to an adjacent cell as a function of time.
- If we plot this using MATLAB, we can represent as in the following graph the concentration of quorum that diffuses to an adjacent cell as a function of time.
- As time goes on, E. coli produces more and more quorum, which diffuses to adjacent E. coli. (Fig 4) Although theory predicts forty quorum molecules are produced per minute, the actual number of quorum molecules present at the site of production (at x = 0) is only around two to three because they diffuse away very rapidly. Although the concentration of quorum tend to be lower at 1.3 um from the site of production, the concentration in both the origin and the destination reaches about 180 molecules as time passes 100 minutes.
- How much quorum does adjacent E. coli receive? In reality, E. coli are not point particles in space. In order to predict the actual amount of quorum in E. coli, it is necessary to integrate q from distance 0 to 0.5 um. For simplicity, we simply add quorums at distances from 0 until 0.5 um at an interval of 0.1 um. To calculate the total amount of quorum dispersed to adjacent cells, we add quorum concentrations from 0.6 to 1.6 um at the same interval of 0.1 um. Because we assume a two dimensional tightly on previous analysis, we simply divide the result by 8 to obtain the amount of quorum that one cell receives.
- After 100 minutes, 920 quorums will be left in the source E. coli, and 2000 quorums will have been dispersed to all adjacent E. coli. (Fig 5) In conclusion, each adjacent E. coli receives one fourth the quorum contained within the source E. coli.
References
- [1] http://appscmaterial.blogspot.com/2011/06/e-coli-outbreak-in-europe.html
- [2] Howard C. Berg, Random Walks in biology, Princeton Paperbacks, New expanded edition (1993)
- [3] A. Kolmogorov et al., Moscow Univ. Bull. Math. A 1 (1937): 1
- [4] R. A. Fisher, Ann. Eug. 7 (1937): 355
- [5] P. C. Fife, Mathematical Aspects of Reacting and Diffusing Systems, Springer (1979)
- [6] Mark R. Tinsley, Annette F. Taylor, Zhaoyang Huang, and Kenneth Showalter, Emergence of Collective Behavior in Groups of Excitable Catalyst-Loaded Particles: Spatiotemporal Dynamical Quorum Sensing, Physical Review Letters, 102, 158301 (2009)
 "
"