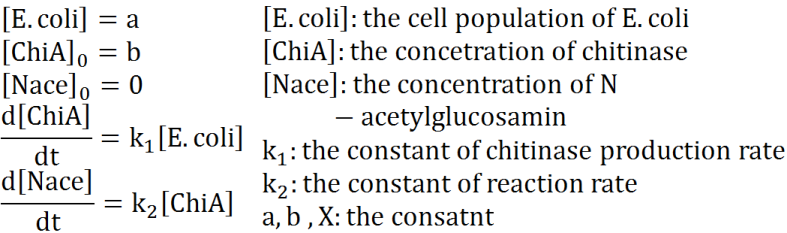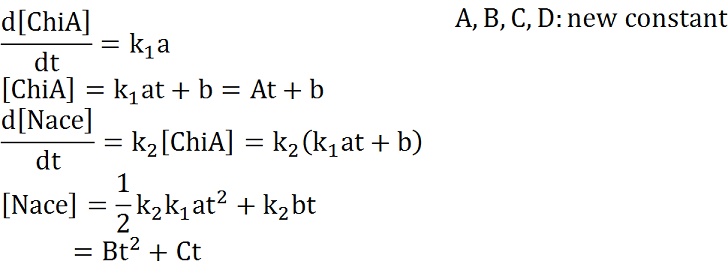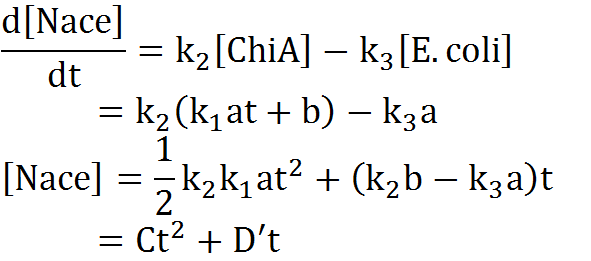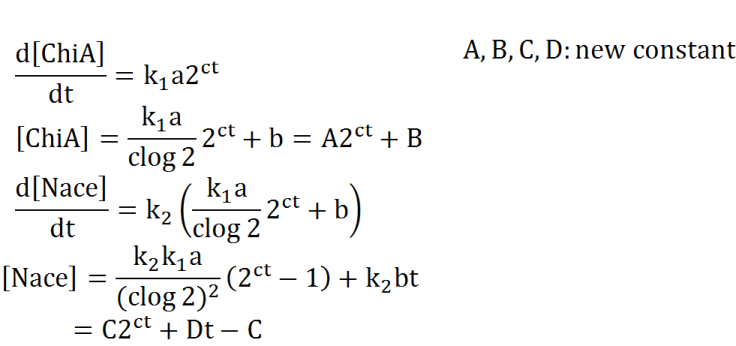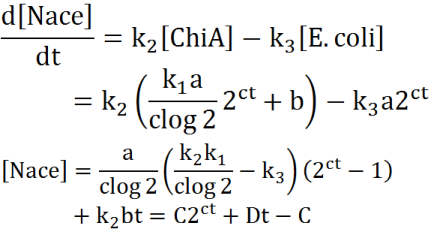Team:Kyoto/Digestion/Modeling
From 2011.igem.org
(→Stable state model) |
(→Stable state model) |
||
| Line 9: | Line 9: | ||
=='''Stable state model'''== | =='''Stable state model'''== | ||
| - | We can apply this model when cell population of E.coli don't change. In this case, we can think about two reasons cell population don't change.<br> | + | We can apply this model when cell population of E.coli don't change. In this case, we can think about two reasons why cell population don't change.<br> |
*First, cell population is too small for us to see the sugnificant difference of cell population.<br> | *First, cell population is too small for us to see the sugnificant difference of cell population.<br> | ||
*Second, nutrients in medium don't sufficenetly exist for E.coli to grow.<br> | *Second, nutrients in medium don't sufficenetly exist for E.coli to grow.<br> | ||
| - | |||
We thought about each reasons and . | We thought about each reasons and . | ||
| - | === | + | ==='''no feedback model'''=== |
We defined these following equations. In defining these equations, we premised the following four things, that is, | We defined these following equations. In defining these equations, we premised the following four things, that is, | ||
*chitinase in medium isn't decomposed | *chitinase in medium isn't decomposed | ||
| Line 39: | Line 38: | ||
[[File:Modeling_Modeling1.jpg]]<br> | [[File:Modeling_Modeling1.jpg]]<br> | ||
| + | ==='''negative feedback'''=== | ||
| - | + | We creat anothre graph. In this graph, E.coli digests N-acetylgulcosamin. Therefore, the speed of increase of the concentration of N-acetylglucosamin is lower than no feedback model. In this model, we used the following equation. | |
[[File:Modeling_Equation3.png]]<br> | [[File:Modeling_Equation3.png]]<br> | ||
| + | |||
Revision as of 02:32, 6 October 2011
Contents |
Digestion Modeling
We preformed modeling to improve usability of the results of Team Digestion.
The aim of these modelings is the creation of the relationship of time and the cell population of E.coli and the concentration of chitinase and N-acetylglucosamin.
We created two models; Stable state model and exponential state model.
Stable state model
We can apply this model when cell population of E.coli don't change. In this case, we can think about two reasons why cell population don't change.
- First, cell population is too small for us to see the sugnificant difference of cell population.
- Second, nutrients in medium don't sufficenetly exist for E.coli to grow.
We thought about each reasons and .
no feedback model
We defined these following equations. In defining these equations, we premised the following four things, that is,
- chitinase in medium isn't decomposed
- E.coli don't digest N-acetylgulcosamin
- chitin as substrate of chitinase is sufficient for reaction with chitinase
- E.coli don't grow.
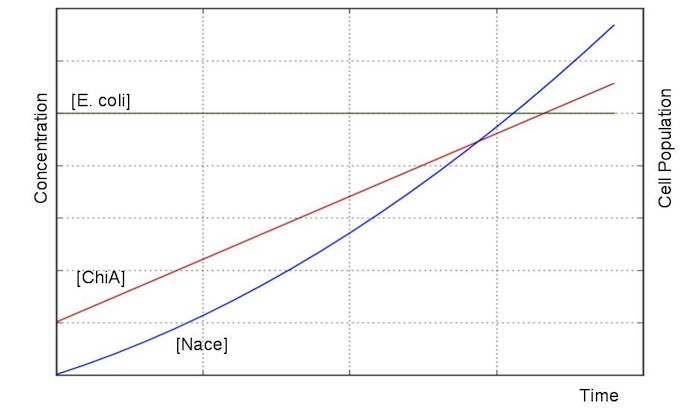
Two under equations of this figure show the production of citinase by E.coli and the decomposition reaction of chitin. In this decompositon reaction, the concentration of chitin isn't related because chitin is solid and don't dissolve in water.
We sought the answers of these equation by followig procedures.
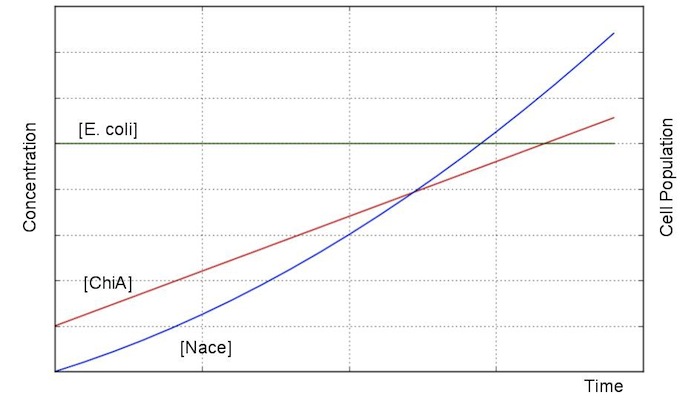
From these answers, we can get this graph.
negative feedback
We creat anothre graph. In this graph, E.coli digests N-acetylgulcosamin. Therefore, the speed of increase of the concentration of N-acetylglucosamin is lower than no feedback model. In this model, we used the following equation.
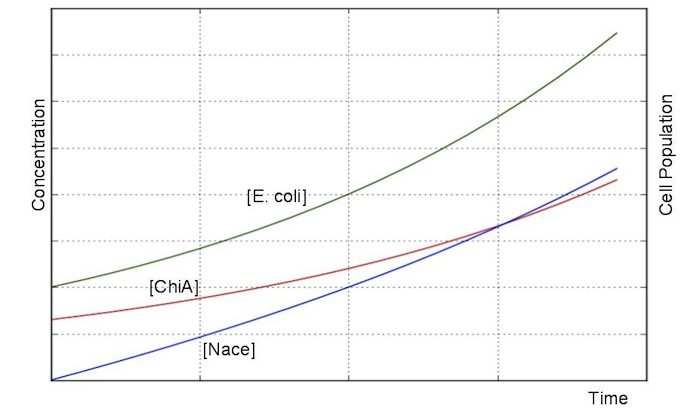
Exponetial state model
At first, we defined these things. In these premises
- chitinase in medium isn't decomposed
- E.coli don't digest N-acetylgulcosamin
- chitin as substrate of chitinase is sufficient for reaction with chitinase
- E.coli grow exponentialy
Two under equations of this figure show the production of citinase by E.coli and the decomposition reaction of chitin. In this decompositon reaction, the concentration of chitin isn't related because chitin is solid and don't dissolve in water.
We sought the answers of these equation by followig procedures.
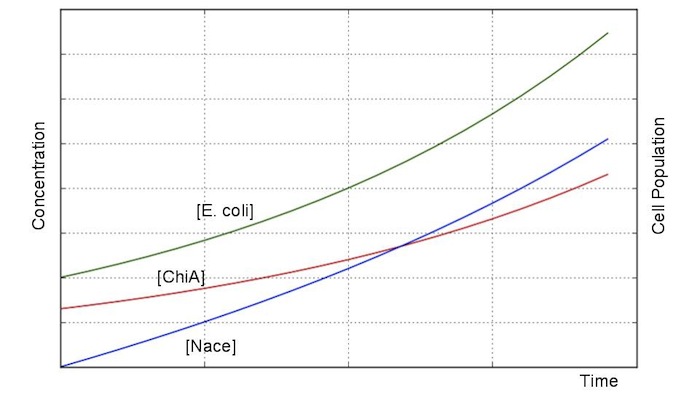
From these answers, we can get this graph.
Second, we creat anothre graph. In this graph, E.coli digest N-acetylgulcosamin. In this model, following equatio was used.
 "
"