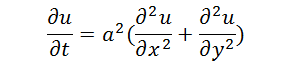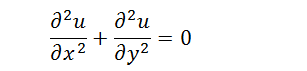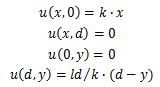Team:Tsinghua/modeling
From 2011.igem.org
(→Formation of concentration gradient) |
|||
| (36 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
{{:Team:Tsinghua/leftbar}} | {{:Team:Tsinghua/leftbar}} | ||
<html> | <html> | ||
| - | |||
<script> | <script> | ||
| - | navl = new Array( | + | navl = new Array("Project", "Experiments", "Modeling"); |
| - | lk = new Array(" | + | lk = new Array("/Team:Tsinghua/project", "/Team:Tsinghua/experiment", "#mdl"); |
writenav(navl, lk); | writenav(navl, lk); | ||
</script> | </script> | ||
| + | <div id="content_box"> | ||
| + | <a id="mdl"></a> | ||
<div id="main_content"> | <div id="main_content"> | ||
| + | </html> | ||
| + | =Modeling= | ||
| + | In order to depict the whole transportation process, models on formation of concentration gradient, E. Coli movement, and transcriptional regulation are essential. | ||
| + | |||
| + | ==Formation of concentration gradient== | ||
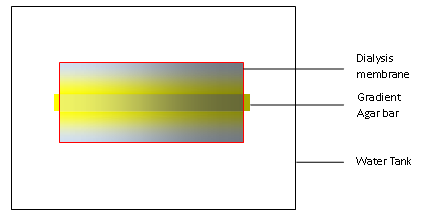
| + | In our experiments, we first build a concentration gradient inside an agar bar as in any other traditional practice. When put in the water, the gradient agar bar will dictate the formation of a concentration gradient in water as solutes inside the agar can diffuse out. We use a dialysis membrane to wrap the bar and some water up, and then stir the water outside the membrane so that excess of solutes can diffuse outside the membrane and maintain the gradient inside the dialysis membrane. | ||
| + | |||
| + | [[File:Thumodel_1.png]] | ||
| + | |||
| + | The effect of dialysis membrane is crucial as shown in the animation here. | ||
| + | |||
| + | |||
| + | <html><object classid="clsid:d27cdb6e-ae6d-11cf-96b8-444553540000" | ||
| + | |||
| + | codebase="http://download.macromedia.com/pub/shockwave/ | ||
| + | cabs/flash/swflash.cab#version=6,0,40,0" | ||
| + | |||
| + | width="468" height="350" | ||
| + | id="mymoviename"> | ||
| + | <param name="movie" | ||
| + | |||
| + | value="https://static.igem.org/mediawiki/2011/b/b1/Thufalsh.swf" /> | ||
| + | |||
| + | <param name="quality" value="high" /> | ||
| + | <embed src="https://static.igem.org/mediawiki/2011/b/b1/Thufalsh.swf" quality="high" bgcolor="#ffffff" width="468" height="350" | ||
| + | name="mymoviename" align="" type="application/x-shockwave-flash" | ||
| + | pluginspage="http://www.macromedia.com/go/getflashplayer"> | ||
| + | |||
| + | |||
| + | </embed> | ||
| + | |||
| + | </object> | ||
| + | </html> | ||
| + | |||
| + | In light of this model, it’s advisable to construct the model for gradient based on diffusion across two surfaces. | ||
| + | |||
| + | Supposing the concentration inside the bar is linear, the length of the agar bar ''l'', and the distance from the dialysis membrane to the bar ''d'', we might set up the coordinate with ''x''-axis along the bar and ''y''-axis perpendicular to the bar. The points close to the bar are on the line ''y=0'', while points close to the dialysis membrane are on the line ''y=d''. | ||
| + | |||
| + | When the concentration is almost steady, we shall assume that the concentration close to the bar is equal to the bar and the concentration close to the dialysis membrane is zero. Hence, concentration ''u'' | ||
| + | |||
| + | [[File:Thumodel_eq1.png]] | ||
| + | |||
| + | [[File:Thumodel_eq2.png]] | ||
| + | |||
| + | The diffusion abides by | ||
| + | |||
| + | [[File:Thumodel_eq3.png]] | ||
| + | |||
| + | When the system is steady, differential of ''u'' by ''t'' is zero. The equation is as follows, | ||
| + | |||
| + | [[File:Thumodel_eq4.png]] | ||
| + | |||
| + | The marginal conditions can be deduced as follows | ||
| + | |||
| + | [[File:Thumodel_eq6.png]] | ||
| + | |||
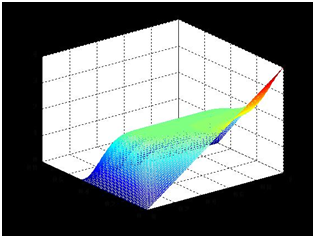
| + | Concentration plot is solved in Matlab2011a with the help of Tsinghua-A Team. | ||
| + | |||
| + | [[File:Thumodel_conc.png]] | ||
| + | |||
| + | The concentration close to the bar is nearly linear, which serves as the basis for our later experiments and modeling. | ||
| + | |||
| + | ==E. Coli movement== | ||
| + | It is known that movement of E. Coli is dependent on phorphorylation/dephorphorylation cycle of CheW protein and consequent shift between swimming forward and tumbling. Based on this mechanism, movement of E. Coli is largely a random process, the probability of which is modulated by certain chemicals. | ||
| + | |||
| + | Assuming that movement of E. Coli is independent of each other, we propose that the probability for E. Coli to change its direction is directly proportional to the concentration of the chemoattractant around while the choice of direction is totally random. | ||
| + | |||
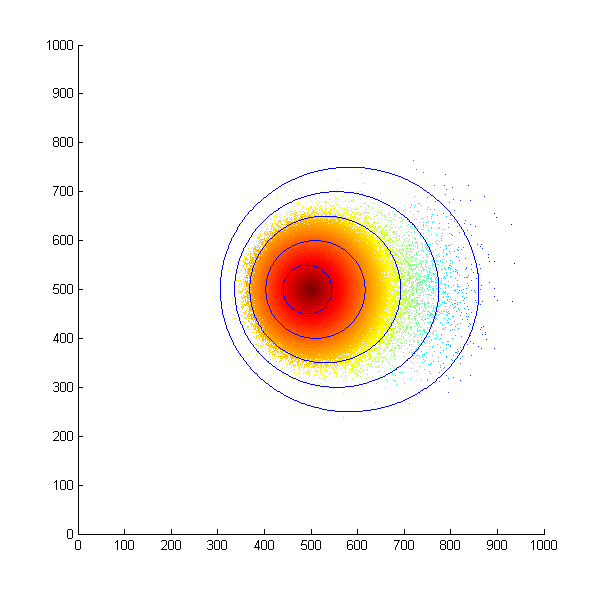
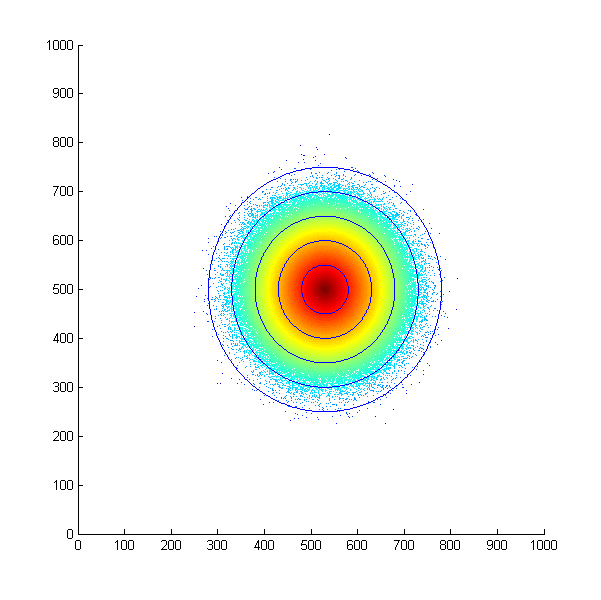
| + | With this assumption in mind, we first simulated the situation that all the bacteria start at the same position and move in a concentration gradient. Every time the bacteria choose to swim, they will move a unit length. The following is the scatter plot after 500 steps. | ||
| + | |||
| + | [[File:Thumodel_eclipse.png|500px]] | ||
| + | |||
| + | ''Simulated E. Coli movement. All the points started from (500, 500) and moved according to the model we proposed. The color from red to blue indicates the distance the bacteria migrated from the starting point. The blue eclipse shows the approximate shape of the colony formed.'' | ||
| + | |||
| + | |||
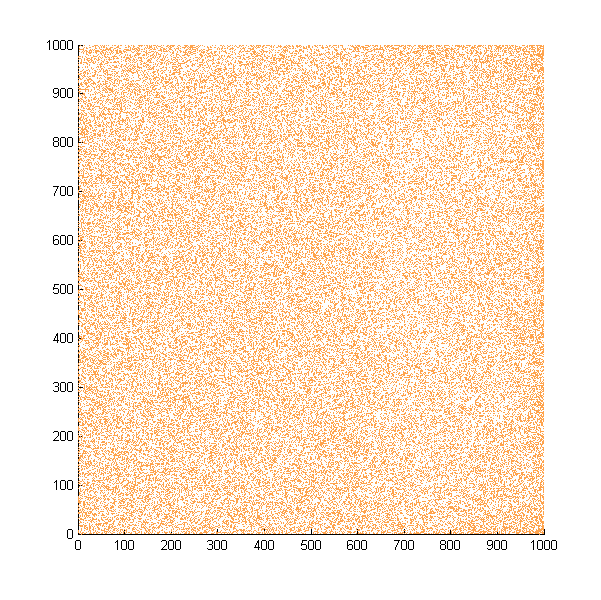
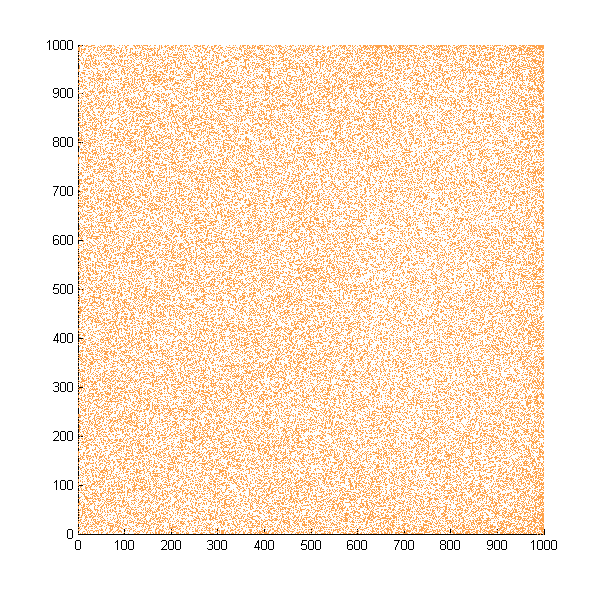
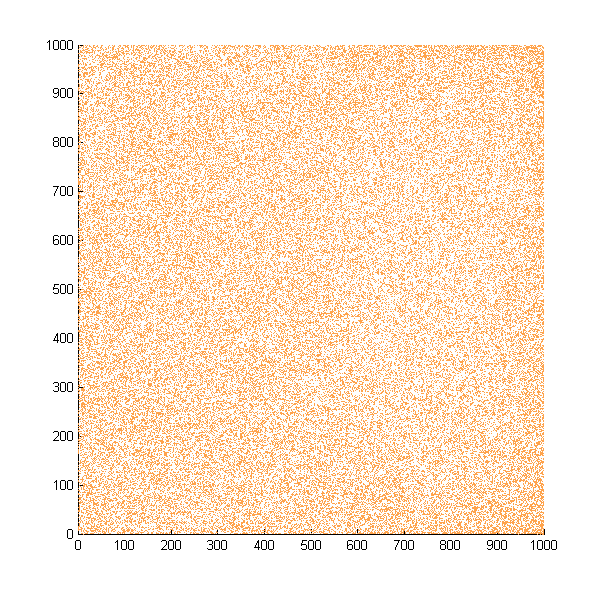
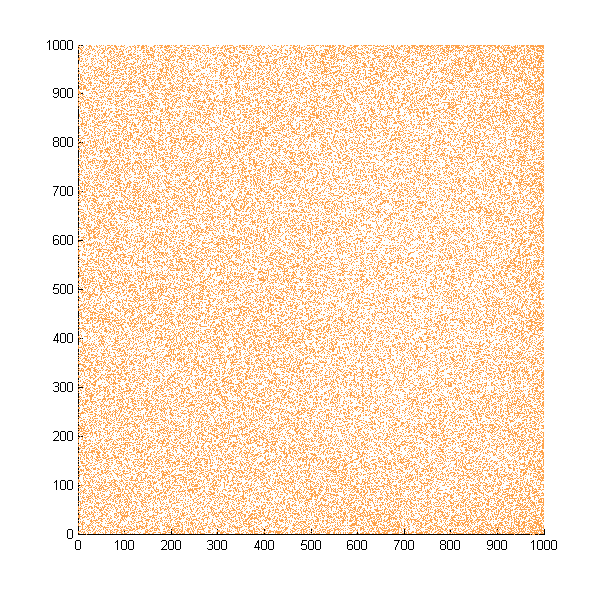
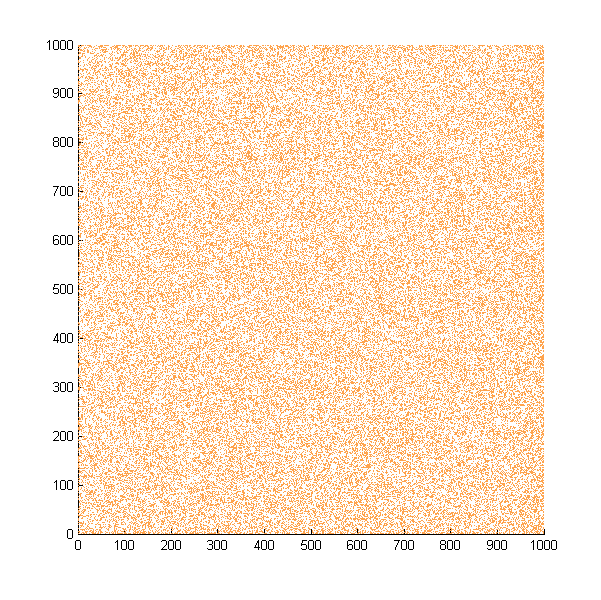
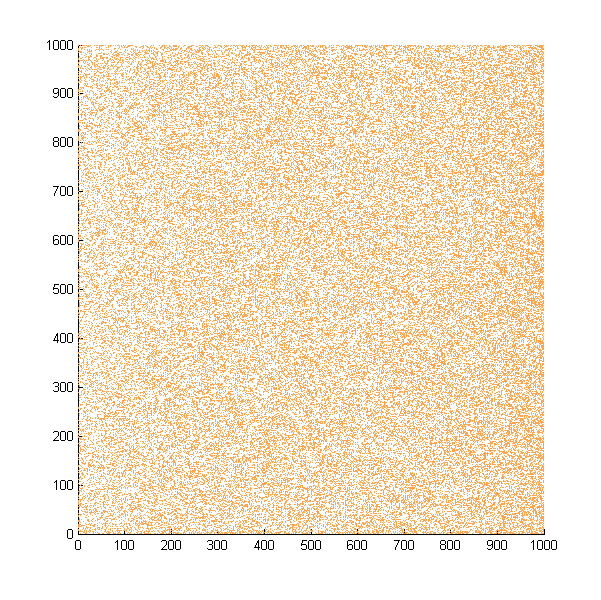
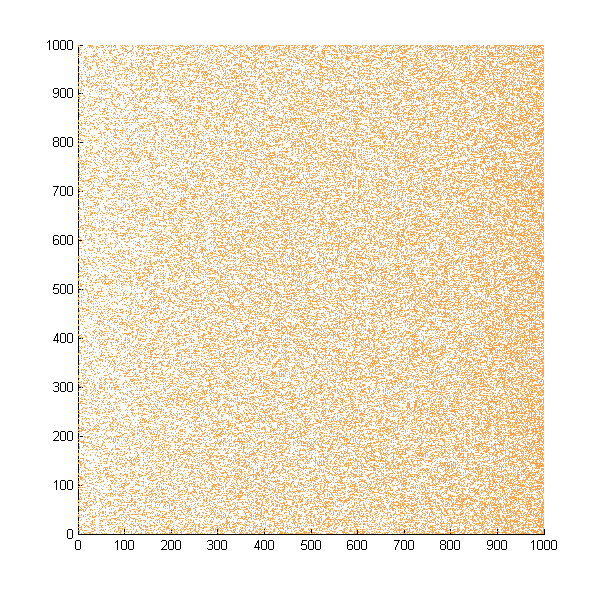
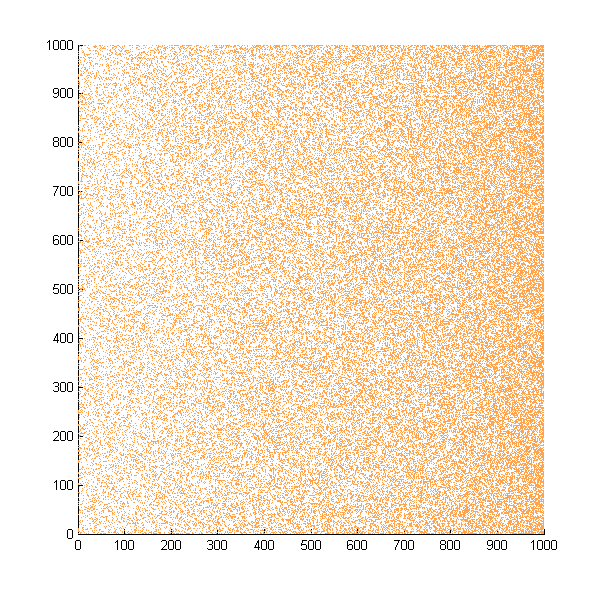
| + | Then we move onto the pattern formed by bacteria in a gradient in liquid. We assume that bacteria was uniformed in the media before the formation of the gradient and plotted the movement after 500, 1000, 1500, 2000, and 2500 steps. | ||
| + | |||
| + | [[File:Thumodel_l1.png|130px]] | ||
| + | [[File:Thumodel_l2.png|130px]] | ||
| + | [[File:Thumodel_l3.png|130px]] | ||
| + | [[File:Thumodel_l4.png|130px]] | ||
| + | [[File:Thumodel_l5.png|130px]] | ||
| + | |||
| + | ''Simulated E. coli movement in liquid. A total of 100,000 cells were uniformly distributed in the liquid at first and the program simulated the migration in a gradient. From x=0 to x=1000, the concentration of the chemoattractant increases, driving bacteria towards the right.'' | ||
| + | |||
| + | ''The region for E. coli to move is from x=0, y=0 to x=1000, y=1000. When a bacterium collides with the boundary, it will choose a new direction randomly. A counter was set to count all the bacteria which have crossed x=1000 at least once.'' | ||
| + | |||
| + | |||
| + | No obvious movement is seen in our simulation, but the counter reported the number of E. Coli that reached the end increases steadily. | ||
| + | |||
| + | {| align="center" style="border: none; background: none; border-spacing: 0;text-align:center;margin-left: 100px;" | ||
| + | ! style="border: 1px solid #39F;padding: 5px;" | Steps from start | ||
| + | ! style="border: 1px solid #39F;padding: 5px;" | Number of bacteria | ||
| + | across the boundary | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 500 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 15671 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 1000 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 31227 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 1500 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 46768 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 2000 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 62123 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 2500 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 77577 | ||
| + | |} | ||
| + | |||
| + | When a bacterium reaches the end, it will randomly turn around. As it will rarely change its direction in the media rich in chemoattractant, it will migrate almost to the midpoint until it makes another turn. We can see that although over 70% cells have reached the end at least once in the last simulation, no accumulation of cells can be seen. Rather, only a small increase in the concentration of bacteria on the right seems visible in this simulation. | ||
| + | |||
| + | Our experimental results verified this point, as no obvious enrichment of bacteria can be seen in the media. However, when we measure OD600 of the two ends of our tubes, we did observe a significant difference. | ||
| + | |||
| + | ==Alternative thinking== | ||
| + | |||
| + | What if E. Coli "knows" the direction of gradient and arbitrarily migrates towards the place with higher attractant concentration? | ||
| + | |||
| + | Tsinghua-A Team helped us built this model. In this model, they assume that each cell has the equal probability of swimming or tumbling, but the direction it finally chooses will be subject to normal distribution with the mean value towards the higher concentration. | ||
| + | |||
| + | The simulation is obviously distinct from the experimental results. When all the cells start from the same point and move in a gradient, a circle not an eclipse is formed. | ||
| + | |||
| + | [[File:Thumodel_nc.png]] | ||
| + | |||
| + | ''Simulated E. Coli movement after 500 steps. The blue circle shows the approximate shape of colony formed.'' | ||
| + | |||
| + | |||
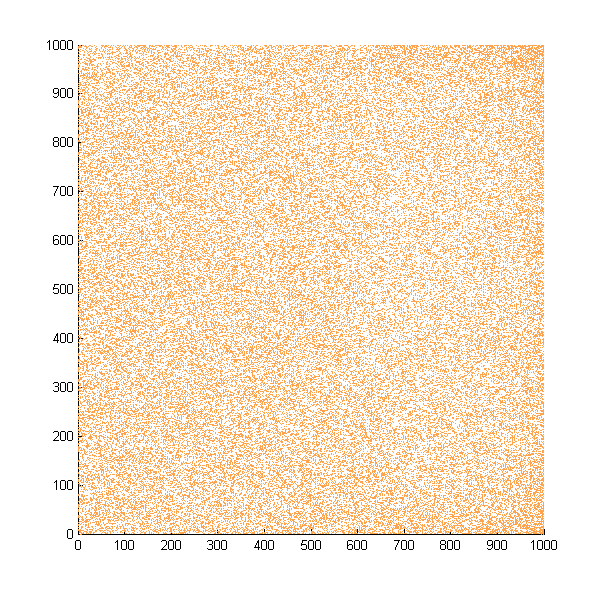
| + | Furthermore, when cells are uniformly distributed in the solution at the beginning, they will migrate towards the target and accumulate at the other end. | ||
| + | |||
| + | [[File:Thumodel_n1.png|130px]] | ||
| + | [[File:Thumodel_n2.png|130px]] | ||
| + | [[File:Thumodel_n3.png|130px]] | ||
| + | [[File:Thumodel_n4.png|130px]] | ||
| + | [[File:Thumodel_n5.png|130px]] | ||
| + | |||
| + | ''Simulate movement in liquid. A total of 100,000 cells are evenly distributed at the beginning. The figures show the distribution after 500, 1000, 1500, 2000, 2500 steps. An obvious accumulation can be seen in this simulation, but not in our experiments. Cells which reach the end of the region in the simulation are forced to take a direction at random. All the cells which reach the end at least once is counted.'' | ||
| + | |||
| + | |||
| + | The cells which reach the end for at least once are counted and listed in the table below. | ||
| + | |||
| + | |||
| + | {| align="center" style="border: none; background: none; border-spacing: 0;text-align:center;margin-left: 100px;" | ||
| + | ! style="border: 1px solid #39F;padding: 5px;" | Steps from start | ||
| + | ! style="border: 1px solid #39F;padding: 5px;" | Number of bacteria | ||
| + | across the boundary | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 500 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 8746 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 1000 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 14545 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 1500 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 20222 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 2000 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 27021 | ||
| + | |- | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 2500 | ||
| + | | style="border: 1px solid #39F;padding: 5px;" | 33916 | ||
| + | |} | ||
| + | |||
| + | |||
| + | Although accumulation of cells is obvious, the actual number of cells which reach the end decrease compared to the previous model. | ||
| - | < | + | This set of results are what most people hope to see, but ''untrue''. It's critical to be objective and rational during modeling, or the result might come out weird. |
| + | <html> | ||
| + | </div> | ||
Latest revision as of 03:56, 6 October 2011

Modeling
In order to depict the whole transportation process, models on formation of concentration gradient, E. Coli movement, and transcriptional regulation are essential.
Formation of concentration gradient
In our experiments, we first build a concentration gradient inside an agar bar as in any other traditional practice. When put in the water, the gradient agar bar will dictate the formation of a concentration gradient in water as solutes inside the agar can diffuse out. We use a dialysis membrane to wrap the bar and some water up, and then stir the water outside the membrane so that excess of solutes can diffuse outside the membrane and maintain the gradient inside the dialysis membrane.
The effect of dialysis membrane is crucial as shown in the animation here.
In light of this model, it’s advisable to construct the model for gradient based on diffusion across two surfaces.
Supposing the concentration inside the bar is linear, the length of the agar bar l, and the distance from the dialysis membrane to the bar d, we might set up the coordinate with x-axis along the bar and y-axis perpendicular to the bar. The points close to the bar are on the line y=0, while points close to the dialysis membrane are on the line y=d.
When the concentration is almost steady, we shall assume that the concentration close to the bar is equal to the bar and the concentration close to the dialysis membrane is zero. Hence, concentration u
The diffusion abides by
When the system is steady, differential of u by t is zero. The equation is as follows,
The marginal conditions can be deduced as follows
Concentration plot is solved in Matlab2011a with the help of Tsinghua-A Team.
The concentration close to the bar is nearly linear, which serves as the basis for our later experiments and modeling.
E. Coli movement
It is known that movement of E. Coli is dependent on phorphorylation/dephorphorylation cycle of CheW protein and consequent shift between swimming forward and tumbling. Based on this mechanism, movement of E. Coli is largely a random process, the probability of which is modulated by certain chemicals.
Assuming that movement of E. Coli is independent of each other, we propose that the probability for E. Coli to change its direction is directly proportional to the concentration of the chemoattractant around while the choice of direction is totally random.
With this assumption in mind, we first simulated the situation that all the bacteria start at the same position and move in a concentration gradient. Every time the bacteria choose to swim, they will move a unit length. The following is the scatter plot after 500 steps.
Simulated E. Coli movement. All the points started from (500, 500) and moved according to the model we proposed. The color from red to blue indicates the distance the bacteria migrated from the starting point. The blue eclipse shows the approximate shape of the colony formed.
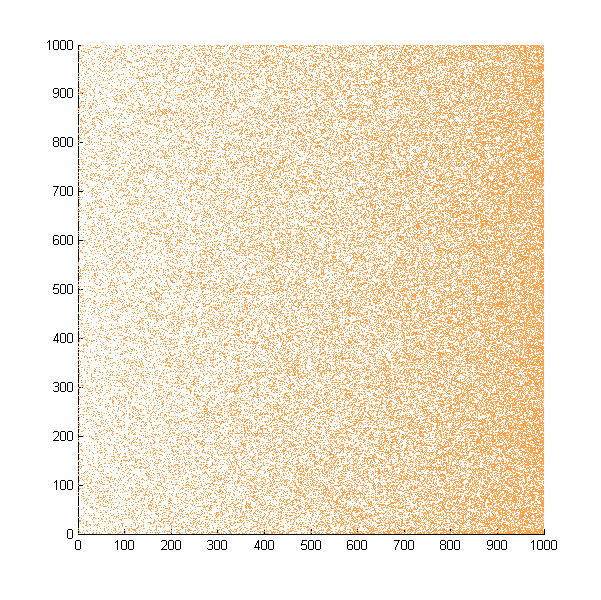
Then we move onto the pattern formed by bacteria in a gradient in liquid. We assume that bacteria was uniformed in the media before the formation of the gradient and plotted the movement after 500, 1000, 1500, 2000, and 2500 steps.
Simulated E. coli movement in liquid. A total of 100,000 cells were uniformly distributed in the liquid at first and the program simulated the migration in a gradient. From x=0 to x=1000, the concentration of the chemoattractant increases, driving bacteria towards the right.
The region for E. coli to move is from x=0, y=0 to x=1000, y=1000. When a bacterium collides with the boundary, it will choose a new direction randomly. A counter was set to count all the bacteria which have crossed x=1000 at least once.
No obvious movement is seen in our simulation, but the counter reported the number of E. Coli that reached the end increases steadily.
| Steps from start | Number of bacteria
across the boundary |
|---|---|
| 500 | 15671 |
| 1000 | 31227 |
| 1500 | 46768 |
| 2000 | 62123 |
| 2500 | 77577 |
When a bacterium reaches the end, it will randomly turn around. As it will rarely change its direction in the media rich in chemoattractant, it will migrate almost to the midpoint until it makes another turn. We can see that although over 70% cells have reached the end at least once in the last simulation, no accumulation of cells can be seen. Rather, only a small increase in the concentration of bacteria on the right seems visible in this simulation.
Our experimental results verified this point, as no obvious enrichment of bacteria can be seen in the media. However, when we measure OD600 of the two ends of our tubes, we did observe a significant difference.
Alternative thinking
What if E. Coli "knows" the direction of gradient and arbitrarily migrates towards the place with higher attractant concentration?
Tsinghua-A Team helped us built this model. In this model, they assume that each cell has the equal probability of swimming or tumbling, but the direction it finally chooses will be subject to normal distribution with the mean value towards the higher concentration.
The simulation is obviously distinct from the experimental results. When all the cells start from the same point and move in a gradient, a circle not an eclipse is formed.
Simulated E. Coli movement after 500 steps. The blue circle shows the approximate shape of colony formed.
Furthermore, when cells are uniformly distributed in the solution at the beginning, they will migrate towards the target and accumulate at the other end.
Simulate movement in liquid. A total of 100,000 cells are evenly distributed at the beginning. The figures show the distribution after 500, 1000, 1500, 2000, 2500 steps. An obvious accumulation can be seen in this simulation, but not in our experiments. Cells which reach the end of the region in the simulation are forced to take a direction at random. All the cells which reach the end at least once is counted.
The cells which reach the end for at least once are counted and listed in the table below.
| Steps from start | Number of bacteria
across the boundary |
|---|---|
| 500 | 8746 |
| 1000 | 14545 |
| 1500 | 20222 |
| 2000 | 27021 |
| 2500 | 33916 |
Although accumulation of cells is obvious, the actual number of cells which reach the end decrease compared to the previous model.
This set of results are what most people hope to see, but untrue. It's critical to be objective and rational during modeling, or the result might come out weird.
 "
"