|
|
| (47 intermediate revisions not shown) |
| Line 5: |
Line 5: |
| | Related Links:</div> | | Related Links:</div> |
| | <div id="boxcontent"><DL> | | <div id="boxcontent"><DL> |
| - | <div class="heading">Vitamin A:</div>
| |
| - | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Project/VitA">Project</a><br/>
| |
| - | <DD><a href="#">Parts</a><br/>
| |
| - | <DD><a href="#">Protocols</a><br/></br/></DL>
| |
| | <div class="heading">Modeling:</div><DL> | | <div class="heading">Modeling:</div><DL> |
| - | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/Platforms">Modeling Platforms</a><br/>
| + | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/Platforms">Modeling Platforms</a><br/> |
| - | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/Methods">Analytic Methods</a><br/>
| + | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/LBSMod">LBS Models</a><br/> |
| - | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/GeneExp">Gene Expression</a><br/> | + | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/Sensitivity">Sensitivity</a><br/> |
| - | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/VitA">Vitamin A</a><br/> | + | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/ParaFit">Parameter fitting</a><br/></DL> |
| - | <DD><a href="https://2011.igem.org/Team:Johns_Hopkins/Modeling/VitC">Vitamin C</a><br/></br/></DL>
| + | |
| | </div> | | </div> |
| | </div> | | </div> |
| Line 20: |
Line 15: |
| | </html> | | </html> |
| | __NOTOC__ | | __NOTOC__ |
| - | ====== LBS: A New Approach to Modeling in iGEM ====== | + | ====== Optimization ====== |
| - | ===== Anatomy of an LBS model: the beta-carotene pathway (vitamin A) =====
| + | We transition from mathematical description to engineering by using optimization techniques to rationally design the most efficient system that meets our specifications. In our case, we are trying to design a strain of yeast that produces a significant amount of vitamins relative to consensus daily value levels while minimizing the amount of enzyme that the cell needs to produce. |
| - | ==== Compartments and species ====
| + | |
| - | Here we declare two compartments under the root "world" compartment. First is the cytosol, inside of which goes the nucleus.
| + | |
| | | | |
| - | We specify ribosomes and RNA polymerases globally because they are shared across all gene expression processes. We then declare the crtE gene which codes for the enzyme GGPP synthase, the crtYB gene which codes for the bifunctional phytoene synthase / lycopene cyclase, and the crtI gene which codes for carotene desaturase. Note that crtB and crtY are usually separate enzymes: phytoene synthase and lycopene cyclase respectively. crtYB is essentially crtB with an active domain from crtY, allowing it to catalyze both these two non-sequential reactions, in addition to a third reaction which converts neurosporene into dihydro-beta-carotene, resulting in a loss of carbon from this pathway.
| + | '''Here we introduce multi-objective optimization to iGEM for the first time. We hope that the narrative below helps team evaluate and implement this powerful technique for their own projects.''' |
| | | | |
| - | Farnesyl diphosphate is the first metabolite that we consider in our synthetic pathway because it is the last metabolite found normally in yeast. We list our other metabolites in their order in the pathway until our final product beta-carotene. We conclude with a list of enzymatic kinetic parameters (K<sub>m</sub> and K<sub>cat</sub> per Michaelis-Menten) and a list of expression kinetic parameters. These lengthy rate declarations are not shown below, but can be seen in the full code.
| + | ''In this discussion we consider optimizing the β-carotene pathway. All analysis done for β-carotene has been duplicated for L-ascorbate as well. Plots for L-ascorbate are also shown.'' |
| | | | |
| - | <pre>
| + | ====== Objectives ====== |
| - | // Compartments
| + | We have used optimization techniques to answer a number of questions. |
| - | comp cytosol = new comp;
| + | * '''What concentration of each enzyme should we attempt to attain in vivo in order to have optimal vitamin production?''' |
| - | comp nucleus = new comp inside cytosol;
| + | * How much vitamin can we expect VitaYeast to produce under different constraints? |
| | + | * What sort of resources will vitamin production demand from the cell? |
| | + | * How will VitaYeast allocate its resources to produce vitamins optimally? |
| | | | |
| - | // Transcriptional machinery
| + | ====== Multi-objective optimization ====== |
| - | spec Ribo = new{mrna:binding};
| + | We began by hypothesizing what sort of results we could expect from optimizing our pathway for maximum β-carotene production. We quickly realized that we were in for a major problem: from the perspective of the optimization algorithm, adding more enzyme is ''always'' right thing to do. Adding enzyme might increase the pathway's speed and efficiency, but would never cause it to slow down. Thus, any decent algorithm would converge on a solution that pushed the enzyme concentrations to their upper bounds. Running optimization in this way would be trivial. |
| - | spec RNAP = new{dna:binding,mrna:binding};
| + | |
| - | // Gene-protein pairs
| + | |
| - | spec crtE = new{bind:binding}; spec GGPP_synth_exo = new{};
| + | |
| - | spec BTS1 = new{bind:binding}; spec GGPP_synth_endo = new{};
| + | |
| - | spec crtYB = new{bind:binding}; spec carotene_desat = new{};
| + | |
| - | spec crtI = new{bind:binding}; spec phytoene_synth_lycopene_cyc = new{};
| + | |
| - | // Metabolites
| + | |
| - | spec farnesyl_PP = new{};
| + | |
| - | spec GGPP = new{};
| + | |
| - | spec phytoene = new{};
| + | |
| - | spec neurosporene = new{};
| + | |
| - | spec lycopene = new{};
| + | |
| - | spec beta_carotene = new{};
| + | |
| - | spec hh_beta_carotene = new{};
| + | |
| - | </pre>
| + | |
| | | | |
| - | ==== Expression ====
| + | We know intuitively that as we demand increasing enzyme production from cells, we strain their resources until the cell viability and overall product output actually decrease. We do not have a quantitative model for this vague notion of "straining" our VitaYeast, so it cannot be incorporated directly into our simulation. We are left with needing to express the "strain" constraint in a more powerful and dynamic way than bounding and simple linear constraints. One solution is to maximize vitamin production while ''simultaneously'' solving the problem of minimizing "strain". Then, for a given level of strain, we know the optimal vitamin production level and vice-versa. |
| - | The first three modules comprise [[modeling:expression#A naive transcriptional model in LBS|our standard expression model]].
| + | |
| - | <pre>
| + | |
| - | module transcribe(spec DNA:{bind}, mRNA:{down}) {...};
| + | |
| - | module translate (spec mRNA:{up}, Prot) {...};
| + | |
| - | module express (comp nuc; spec DNA:{bind}, Prot) {...};
| + | |
| - | </pre>
| + | |
| | | | |
| - | ==== Simple reaction module ==== | + | ===== Pareto Front ===== |
| - | We create a module to handle simple reactions in which an enzyme converts a single substrate to a single product. All metabolic reactions that we are interested in follow the Michaelis-Menten pattern outlined below. Note that the rate here is not a rate constant as it would be in mass action kinetics, but is instead the Michaelis-Menten rate expression.
| + | In biology, like engineering, it is not rare to require the attainment of different and possibly conflicting objectives; for example, reaching a place as fast as possible with minimum fuel consumption. Multi-objective optimization aims to identify the largest set of trade-off solutions, using the well known financial principle of Pareto optimality. Multi-objective optimization yields a set of Pareto-optimal solutions from all feasible solutions such that an improvement in any single objective causes a worsening of another objective. Such points are said to lie approximately on the Pareto frontier: a surface in the objective function space containing all the Pareto-optimal points. |
| - | <pre>
| + | |
| - | module mmRXN(spec sub, enz, prod; rate km, kcat) {
| + | |
| - | rate rxn_rate = kcat*enz/(sub+km);
| + | |
| - | sub + enz ->[rxn_rate] enz + prod
| + | |
| - | };
| + | |
| - | </pre>
| + | |
| | | | |
| - | ==== Expression and reaction module invocations ====
| + | We are interested in solving the following multi-objective problem: how can we maximize the amount of vitamin produced while minimizing the extra nitrogen required to produce the enzyme. Nitrogen usage serves as a proxy for the general burden of making extra enzymes out of amino acids. We quickly calculated the [https://2011.igem.org/Team:Johns_Hopkins/Modeling/Nitro nitrogen content] of each enzyme in our pathways. |
| - | This is the heart of the code where we tell LBS to actually simulate something. We invoke the expression module on our two gene-enzyme pairs and the reaction modules for the metabolites that our enzymes process. We then explicitly degrade our enzymes at a uniform rate. The vertical pipes are parallel operators which tell LBS to evaluate these reactions in parallel. In the actual code, all the code below is encapsulated in cytosol[...].
| + | |
| | | | |
| - | It is important to note that our model greatly oversimplifies the complexity of the reactions. Each conversion between metabolites involves between 2 and 4 separate reactions. However, these reactions tend to be very fast. While the enzymes in our pathway are considered to catalyze all steps of these reactions, the overall rate is controlled by the enzyme's ability to catalyze a single rate-limiting reaction. In fact, the other minor reaction rates are often not even measurable. You will note one exception below in the case of carotene desaturase. Carotene desaturase converts phytoene to neurosporene at a rate of about 120 per second. It then converts neurosporene to lycopene at a rate of about 10 per second. Even though we model both reactions explicitly, the observation that one reaction is an order of magnitude slower than the other supports the single rate-limiting step simplification.
| + | ===== Experimental Setup ===== |
| - | <pre>
| + | In order to take advantage of Matlab's many built-in optimization and analysis tools, we translated our LBS models into models in Matlab's SimBiology Toolbox. The Toolbox lets us generate SBML files which can be loaded into your modeling package of choice. |
| - | express(nucleus, crtE:{bind}, GGPP_synth_exo) |
| + | |
| - | express(nucleus, BTS1:{bind}, GGPP_synth_endo) |
| + | |
| - | express(nucleus, crtYB:{bind}, phytoene_synth_lycopene_cyc) |
| + | |
| - | express(nucleus, crtI:{bind}, carotene_desat) |
| + | |
| - | mmRXN(farnesyl_PP, GGPP_synth_endo, GGPP, GGPP_synth_endo_Km, GGPP_synth_endo_Kcat) |
| + | |
| - | mmRXN(farnesyl_PP, GGPP_synth_exo, GGPP, GGPP_synth_exo_Km, GGPP_synth_exo_Kcat) |
| + | |
| - | mmRXN(GGPP, phytoene_synth_lycopene_cyc, phytoene, phytoene_synth_Km, phytoene_synth_Kcat) |
| + | |
| - | mmRXN(phytoene, carotene_desat, neurosporene, carotene_desat_neurosporene_Km,
| + | |
| - | carotene_desat_neurosporene_Kcat) |
| + | |
| - | mmRXN(neurosporene, carotene_desat, lycopene, carotene_desat_lycopene_Km,
| + | |
| - | carotene_desat_lycopene_Kcat) |
| + | |
| - | mmRXN(neurosporene, carotene_desat, hh_beta_carotene,
| + | |
| - | phytoene_synth_hh_beta_carotene_Km, phytoene_synth_hh_beta_carotene_Kcat) |
| + | |
| - | mmRXN(lycopene, phytoene_synth_lycopene_cyc, beta_carotene,
| + | |
| - | phytoene_synth_beta_carotene_Km, phytoene_synth_beta_carotene_Kcat) |
| + | |
| - | GGPP_synth_exo ->{prot_deg} |
| + | |
| - | GGPP_synth_endo ->{prot_deg} |
| + | |
| - | carotene_desat ->{prot_deg} |
| + | |
| - | phytoene_synth_lycopene_cyc ->{prot_deg} |
| + | |
| - | </pre>
| + | |
| | | | |
| - | ==== Initial conditions ====
| + | SMBL models: |
| - | We establish initial conditions for our system, namely 5 copies of each gene and a very limited number of ribosomes and RNA polymerases. We take the numbers here to mean "the number of ribosomes or RNA polymerases made available to the expression process of our genes of interest". There are of course many times more ribosomes and polymerases in the cell, but they are working on making other proteins. Only a small portion is ever free to deal with our synthetic construct.
| + | [[File:Beta-carotene pathway.zip|Vitamin A]] | [[File:L-ascorbate pathway.zip|Vitamin C]] |
| | | | |
| - | In addition, the first line below is a black-box input: a certain number of our initial substrate is dumped into our system each turn by the cell. We are not interested in modeling the process of how it comes about, we only care about the result and what our system does to this exogenous input.
| + | The first multi-objective optimizer we explored is Matlab's built-in genetic algorithm "gamultiobj", which is based on the NSGA-II algorithm. When we run this optimizer, it generates a population of 100 "individuals" which code for certain enzyme production levels. For each individual a 30-minute simulation of the pathway is run, yielding the β-carotene production level. A separate function figures out how much nitrogen was used. Combined, the β-carotene production and nitrogen usage constitute that population member's "fitness". The algorithm keeps fit individuals and "breeds" them. |
| - | <pre>
| + | |
| - | ->{1} farnesyl_PP |
| + | [[Image:Beta-carotene_opto_points.png|thumb|275px|left|β-carotene pathway Pareto front]] |
| - | init Ribo 10 |
| + | [[Image:L-Ascorbate_opto.png|thumb|275px|L-ascorbate pathway Pareto front]] |
| - | nucleus[
| + | |
| - | init crtE 5 |
| + | |
| - | init crtYB 5 |
| + | |
| - | init crtI 5 |
| + | [[Image:Simspeed.png|thumb|300px]] |
| - | init RNAP 1
| + | |
| - | ]
| + | Simulating years of time is no small feat. We started by using [http://lepton.research.microsoft.com/webgec/ Visual GEC], which is the native environment for simulating [https://2011.igem.org/Team:Johns_Hopkins/Modeling/LBSMod LBS models]. Visual GEC uses the [http://en.wikipedia.org/wiki/Gillespie_algorithm Gillespie algorithm], a stochastic simulator that has many run-time advantages over standard ODE solvers. But Visual GEC is restricted to running in Microsoft Silverlight: a serious drawback for performance simulation. To make our optimization goals computationally tractable, we ported our models to Matlab's SimBiology toolbox. This allowed us to pre-compile our model to C++ code. Further, our optimization algorithm ran multiple simulation runs in parallel, taking advantage of modern multi-core architectures. The result was a lightening-fast single-run simulation time. |
| - | </pre>
| + | |
| | + | ====== Allocation analysis ====== |
| | + | |
| | + | The graphic above tells us a lot about what goes in (nitrogen) and what comes out (vitamin) of our system, but we are left with somewhat of a black box. We know how much nitrogen gets used and that this usage is optimal, but how does our virtual cell choose to allocate this nitrogen between the various enzymes? What determines this choice? Since the optimizer explicitly minimizes nitrogen usage and maximizes vitamin production, it seems reasonable that our virtual cell is trying to balance each enzyme's usefulness in synthesizing vitamins with the nitrogen cost to produce it. Perhaps one of these two factors dominates the decision. |
| | + | |
| | + | Lets start by looking at how much of each enzyme simulated VitaYeast made as we gave it more nitrogen to work with. |
| | + | |
| | + | [[Image:Bc nitro alloc.png|thumb|275px|left|β-carotene nitrogen allocation]] |
| | + | [[Image:La nitro alloc.png|thumb|275px|L-ascorbate nitrogen allocation]] |
| | + | |
| | + | <!--'''Philosophical side-note:'''<html><br></html> |
| | + | Consider the fact that we are using a ''genetic'' algorithm to determine which strain of yeast is the most fit with respect to vitamin production. In a figurative sense we are simulating not just the vitamin production pathway, but the ''entire natural history'' of a synthetic yeast strain, which, until recently, has only existed in silico. Synthetic biology is about bridging the biological-computational gap in both directions: making cells that can compute and making computers that evolve.--> |
| | + | |
| | + | After simulating the real-time equivalent of ''years'', the algorithm returns a large set of individuals that approximate the Pareto frontier. No individual can make more β-carotene without spending more nitrogen. |
| | + | |
| | + | As we can see, this plot is pretty noisy. For marginal increases in nitrogen usage, the simulated VitaYeast seems to shift the allocations with a bit of randomness. We interpret this as a result of the model not being very [https://2011.igem.org/Team:Johns_Hopkins/Modeling/Nitro nitrogen content sensitive] to the amounts of enzyme made. Consider adding 1000 nitrogen atoms to the system. That's a difference of only one or two enzyme molecules no matter how it is allocated. The difference between adding it to GGPP_synth_endo versus GGPP_synth_exo is likely erased by rounding error. Thus, for small increases in nitrogen allocation, the simulated VitaYeast is indifferent to how it is allocated, resulting in noise. |
| | + | |
| | + | ===== Marginal allocation ===== |
| | + | Despite the noise, we still see clear overall trends, such as the low levels of GGPP_synth_endo used in the optimal solutions. We make these trends explicit with a linear fit to each of the curves above. The slope of the fitted curves is the ''marginal nitrogen allocation'', or the portion of each additional unit of nitrogen allocated to each enzyme. A good way to summarize VitaYeast's allocation decisions is to look at the ratios of the marginal allocations below. |
| | + | |
| | + | [[Image:Bc_nitro_marginal.png|thumb|275px|left|β-carotene marginal nitrogen allocation]] |
| | + | [[Image:La_nitro_marginal.png|thumb|275px|L-ascorbate marginal nitrogen allocation]] |
| | + | |
| | + | ===== Normalized marginal allocation ===== |
| | + | The marginal allocation represents the amount of enzyme made, not the actual nitrogen allocation. For example, every molecule of phytoene-cyclase/lycopene-synthase made requires almost twice as much nitrogen as each molecule of endogenous GGPP synthase. To understand exactly where the nitrogen is going, we need to examine the molecule-wise allocation of nitrogen. So we also plot the fraction of a marginal nitrogen atom allocated to each enzyme. We can see that the bifunctional cyclase/synthase receives a very large portion of the nitrogen, both because it is a large enzyme and because it is important, as seen in the marginal allocation below. |
| | + | |
| | + | [[Image:Bc nitro marginal frac.png|thumb|275px|left|Fraction of each nitrogen atom allocated to each β-cartoene production enzyme]] |
| | + | [[Image:La nitro marginal frac.png|thumb|275px|Fraction of each nitrogen atom allocated to each L-ascorbate production enzyme]] |
| | + | |
| | + | ===== Conclusions ===== |
| | + | We initially set out to use our optimization results to solve for the genetic construct we would need in order to reproduce optimal VitaYeast in vitro. We have gotten as far as finding the optimal enzyme concentrations needed, but developing an accurate model of enzyme expression from DNA is tricky. VitaYeast uses enzymes not native to yeast. How quickly do these enzymes degrade in their new host? How stable is their mRNA? Without this information, we have little hope of figuring out how to fine-tune our enzyme expression levels. The best we can do is to try to express all the enzymes in the right ratio. Looking at the marginal allocation data, we can see which genes we might be interested in including multiple copies of or using stronger promoters. We believe this rough approximation would be a significant improvement over simply placing all genes in identical constructs. Thus in the future we plan on actually testing out the conclusions drawn from optimization in vitro by trying to attain the optimal enzyme concentrations through trial and error. |
| | + | |
| | + | Despite the inability to suggest precise expression parameters, our analysis gave us a good deal of insight into the workings of our pathway. Perhaps this analysis could be applied to natural pathways and larger-scale metabolic networks in order to understand the allocation decisions that drive them. |
| | | | |
| | | | |
| | <html> | | <html> |
| | </div> | | </div> |
Optimization
We transition from mathematical description to engineering by using optimization techniques to rationally design the most efficient system that meets our specifications. In our case, we are trying to design a strain of yeast that produces a significant amount of vitamins relative to consensus daily value levels while minimizing the amount of enzyme that the cell needs to produce.
Here we introduce multi-objective optimization to iGEM for the first time. We hope that the narrative below helps team evaluate and implement this powerful technique for their own projects.
In this discussion we consider optimizing the β-carotene pathway. All analysis done for β-carotene has been duplicated for L-ascorbate as well. Plots for L-ascorbate are also shown.
Objectives
We have used optimization techniques to answer a number of questions.
- What concentration of each enzyme should we attempt to attain in vivo in order to have optimal vitamin production?
- How much vitamin can we expect VitaYeast to produce under different constraints?
- What sort of resources will vitamin production demand from the cell?
- How will VitaYeast allocate its resources to produce vitamins optimally?
Multi-objective optimization
We began by hypothesizing what sort of results we could expect from optimizing our pathway for maximum β-carotene production. We quickly realized that we were in for a major problem: from the perspective of the optimization algorithm, adding more enzyme is always right thing to do. Adding enzyme might increase the pathway's speed and efficiency, but would never cause it to slow down. Thus, any decent algorithm would converge on a solution that pushed the enzyme concentrations to their upper bounds. Running optimization in this way would be trivial.
We know intuitively that as we demand increasing enzyme production from cells, we strain their resources until the cell viability and overall product output actually decrease. We do not have a quantitative model for this vague notion of "straining" our VitaYeast, so it cannot be incorporated directly into our simulation. We are left with needing to express the "strain" constraint in a more powerful and dynamic way than bounding and simple linear constraints. One solution is to maximize vitamin production while simultaneously solving the problem of minimizing "strain". Then, for a given level of strain, we know the optimal vitamin production level and vice-versa.
Pareto Front
In biology, like engineering, it is not rare to require the attainment of different and possibly conflicting objectives; for example, reaching a place as fast as possible with minimum fuel consumption. Multi-objective optimization aims to identify the largest set of trade-off solutions, using the well known financial principle of Pareto optimality. Multi-objective optimization yields a set of Pareto-optimal solutions from all feasible solutions such that an improvement in any single objective causes a worsening of another objective. Such points are said to lie approximately on the Pareto frontier: a surface in the objective function space containing all the Pareto-optimal points.
We are interested in solving the following multi-objective problem: how can we maximize the amount of vitamin produced while minimizing the extra nitrogen required to produce the enzyme. Nitrogen usage serves as a proxy for the general burden of making extra enzymes out of amino acids. We quickly calculated the nitrogen content of each enzyme in our pathways.
Experimental Setup
In order to take advantage of Matlab's many built-in optimization and analysis tools, we translated our LBS models into models in Matlab's SimBiology Toolbox. The Toolbox lets us generate SBML files which can be loaded into your modeling package of choice.
SMBL models:
File:Beta-carotene pathway.zip | File:L-ascorbate pathway.zip
The first multi-objective optimizer we explored is Matlab's built-in genetic algorithm "gamultiobj", which is based on the NSGA-II algorithm. When we run this optimizer, it generates a population of 100 "individuals" which code for certain enzyme production levels. For each individual a 30-minute simulation of the pathway is run, yielding the β-carotene production level. A separate function figures out how much nitrogen was used. Combined, the β-carotene production and nitrogen usage constitute that population member's "fitness". The algorithm keeps fit individuals and "breeds" them.
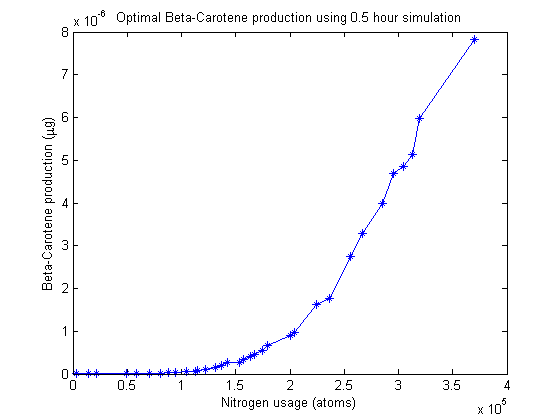
β-carotene pathway Pareto front
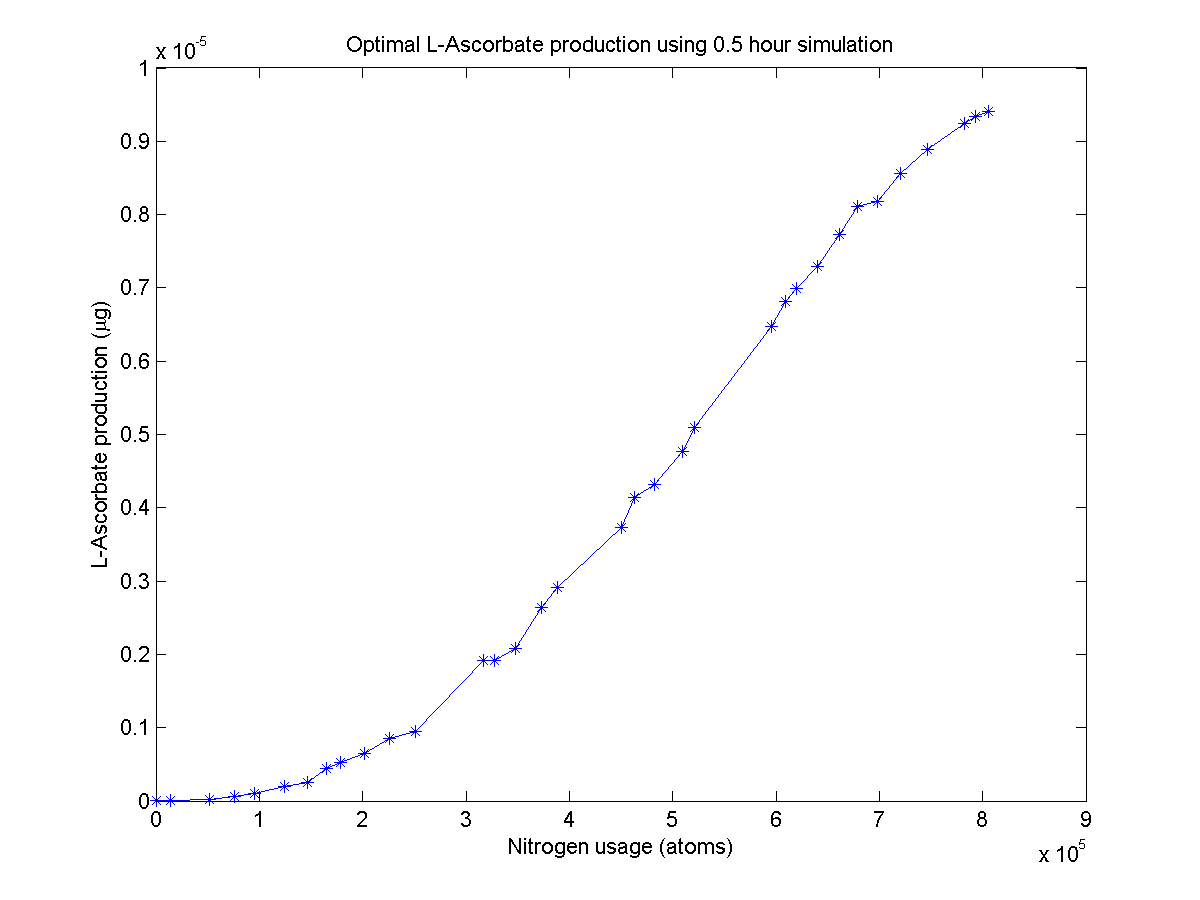
L-ascorbate pathway Pareto front
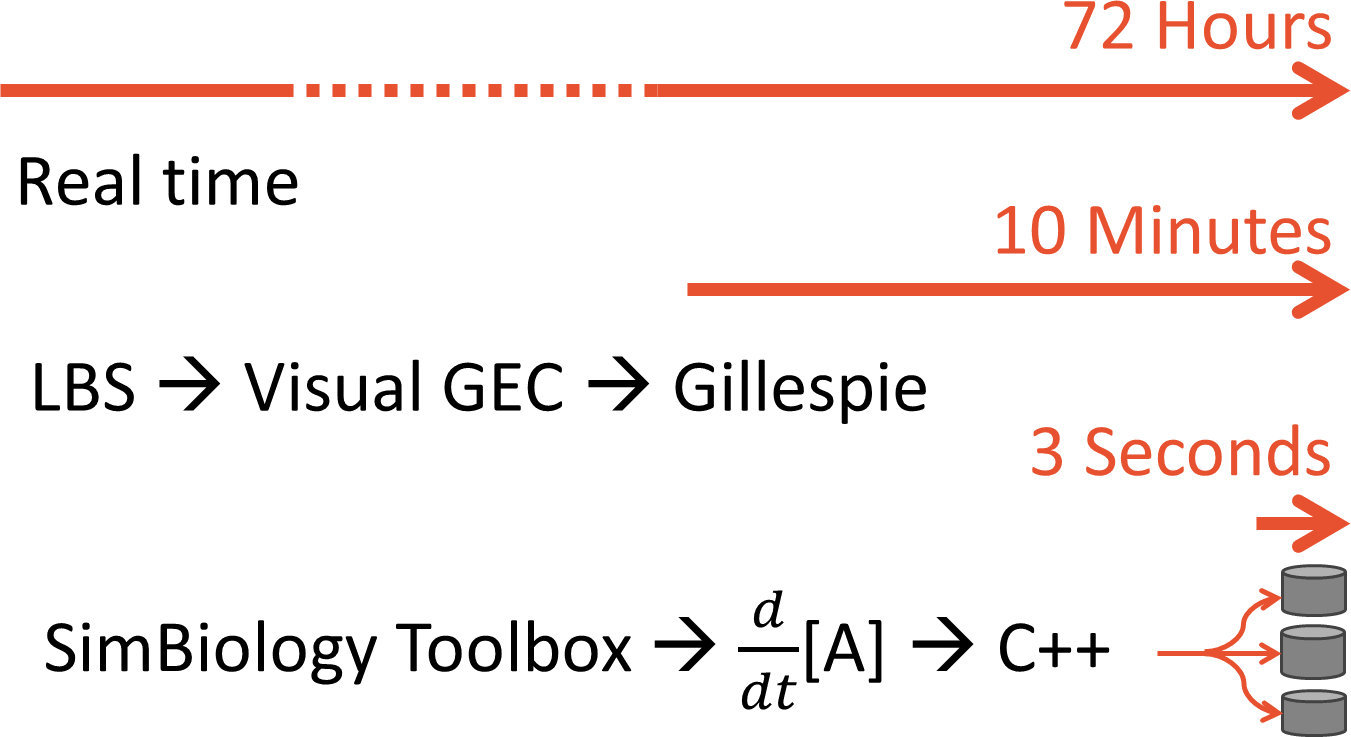
Simulating years of time is no small feat. We started by using [http://lepton.research.microsoft.com/webgec/ Visual GEC], which is the native environment for simulating LBS models. Visual GEC uses the [http://en.wikipedia.org/wiki/Gillespie_algorithm Gillespie algorithm], a stochastic simulator that has many run-time advantages over standard ODE solvers. But Visual GEC is restricted to running in Microsoft Silverlight: a serious drawback for performance simulation. To make our optimization goals computationally tractable, we ported our models to Matlab's SimBiology toolbox. This allowed us to pre-compile our model to C++ code. Further, our optimization algorithm ran multiple simulation runs in parallel, taking advantage of modern multi-core architectures. The result was a lightening-fast single-run simulation time.
Allocation analysis
The graphic above tells us a lot about what goes in (nitrogen) and what comes out (vitamin) of our system, but we are left with somewhat of a black box. We know how much nitrogen gets used and that this usage is optimal, but how does our virtual cell choose to allocate this nitrogen between the various enzymes? What determines this choice? Since the optimizer explicitly minimizes nitrogen usage and maximizes vitamin production, it seems reasonable that our virtual cell is trying to balance each enzyme's usefulness in synthesizing vitamins with the nitrogen cost to produce it. Perhaps one of these two factors dominates the decision.
Lets start by looking at how much of each enzyme simulated VitaYeast made as we gave it more nitrogen to work with.
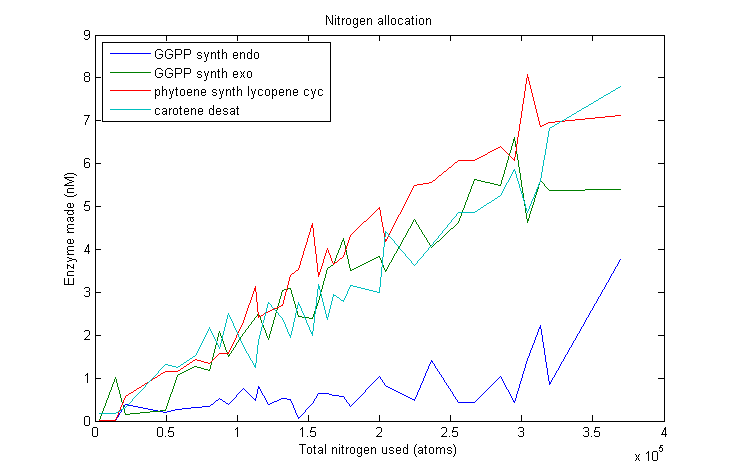
β-carotene nitrogen allocation
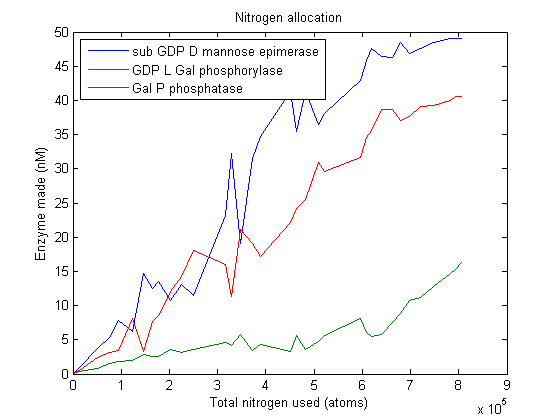
L-ascorbate nitrogen allocation
After simulating the real-time equivalent of years, the algorithm returns a large set of individuals that approximate the Pareto frontier. No individual can make more β-carotene without spending more nitrogen.
As we can see, this plot is pretty noisy. For marginal increases in nitrogen usage, the simulated VitaYeast seems to shift the allocations with a bit of randomness. We interpret this as a result of the model not being very nitrogen content sensitive to the amounts of enzyme made. Consider adding 1000 nitrogen atoms to the system. That's a difference of only one or two enzyme molecules no matter how it is allocated. The difference between adding it to GGPP_synth_endo versus GGPP_synth_exo is likely erased by rounding error. Thus, for small increases in nitrogen allocation, the simulated VitaYeast is indifferent to how it is allocated, resulting in noise.
Marginal allocation
Despite the noise, we still see clear overall trends, such as the low levels of GGPP_synth_endo used in the optimal solutions. We make these trends explicit with a linear fit to each of the curves above. The slope of the fitted curves is the marginal nitrogen allocation, or the portion of each additional unit of nitrogen allocated to each enzyme. A good way to summarize VitaYeast's allocation decisions is to look at the ratios of the marginal allocations below.
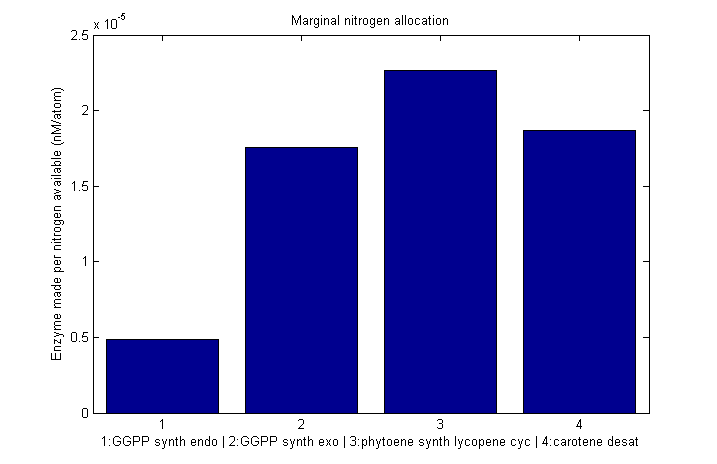
β-carotene marginal nitrogen allocation

L-ascorbate marginal nitrogen allocation
Normalized marginal allocation
The marginal allocation represents the amount of enzyme made, not the actual nitrogen allocation. For example, every molecule of phytoene-cyclase/lycopene-synthase made requires almost twice as much nitrogen as each molecule of endogenous GGPP synthase. To understand exactly where the nitrogen is going, we need to examine the molecule-wise allocation of nitrogen. So we also plot the fraction of a marginal nitrogen atom allocated to each enzyme. We can see that the bifunctional cyclase/synthase receives a very large portion of the nitrogen, both because it is a large enzyme and because it is important, as seen in the marginal allocation below.
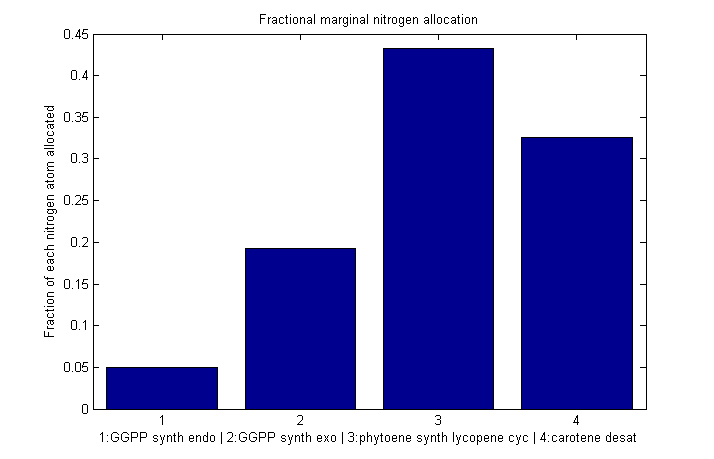
Fraction of each nitrogen atom allocated to each β-cartoene production enzyme
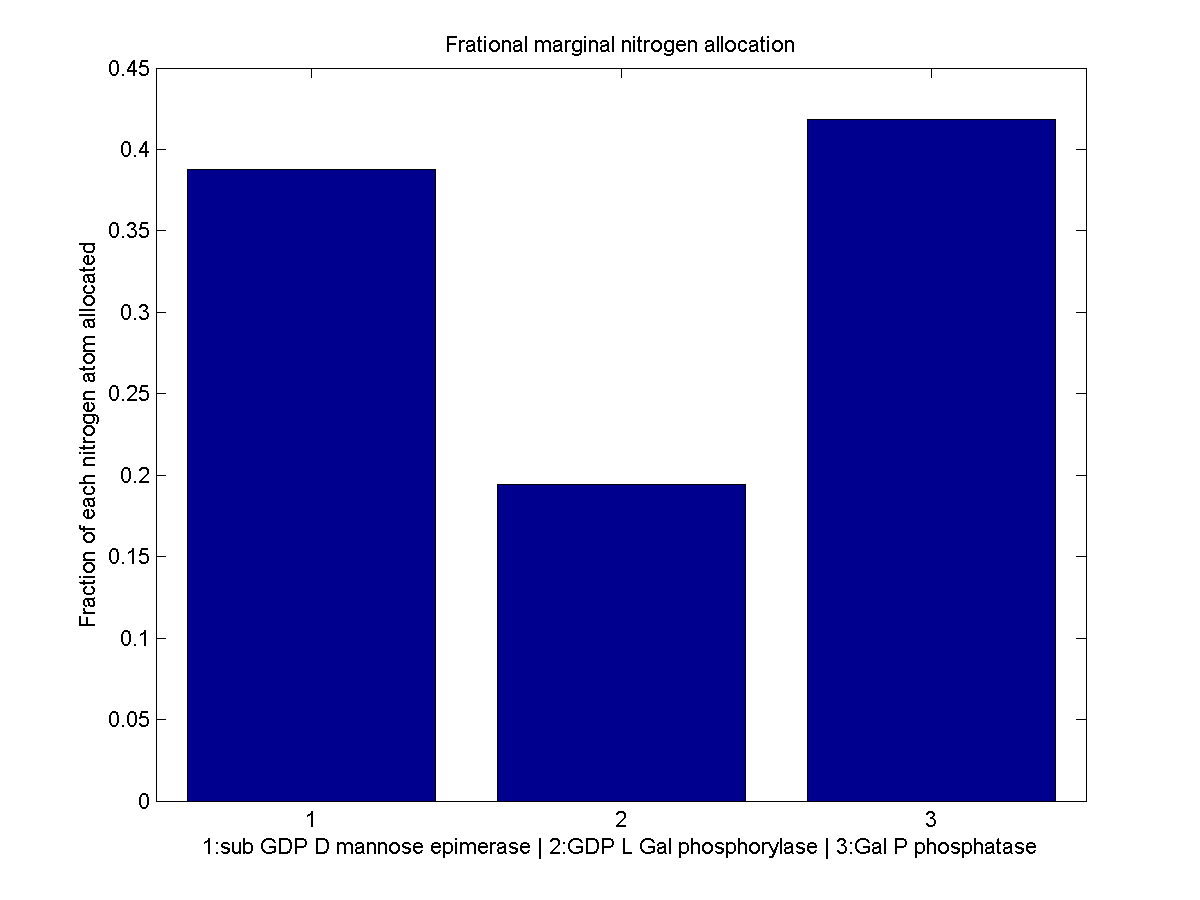
Fraction of each nitrogen atom allocated to each L-ascorbate production enzyme
Conclusions
We initially set out to use our optimization results to solve for the genetic construct we would need in order to reproduce optimal VitaYeast in vitro. We have gotten as far as finding the optimal enzyme concentrations needed, but developing an accurate model of enzyme expression from DNA is tricky. VitaYeast uses enzymes not native to yeast. How quickly do these enzymes degrade in their new host? How stable is their mRNA? Without this information, we have little hope of figuring out how to fine-tune our enzyme expression levels. The best we can do is to try to express all the enzymes in the right ratio. Looking at the marginal allocation data, we can see which genes we might be interested in including multiple copies of or using stronger promoters. We believe this rough approximation would be a significant improvement over simply placing all genes in identical constructs. Thus in the future we plan on actually testing out the conclusions drawn from optimization in vitro by trying to attain the optimal enzyme concentrations through trial and error.
Despite the inability to suggest precise expression parameters, our analysis gave us a good deal of insight into the workings of our pathway. Perhaps this analysis could be applied to natural pathways and larger-scale metabolic networks in order to understand the allocation decisions that drive them.
 "
"