Team:Grenoble/Projet/Modelling/Deterministic

From 2011.igem.org

(Difference between revisions)
 
(19 intermediate revisions not shown)
Line 6: Line 6:
<html>
<html>
 +
 +
<!--
 +
<img src="http://www.clickartists.org/clicksite/html/images/square.jpg"/>
 +
<h2>JB</h2>
 +
 +
 +
<!--
 +
Si vous éditez la page commencez par décommenter ces lignes, publier, PUIS commencer à faire ce que vous avez à faire et quand vous avez fini de publier remettez en commentaire.
 +
 +
Ne laissez pas le carré trop longtemps si vous n'éditez pas, chaque fois reprenez ce qui est sur internet plutôt que ce que vous avez sur votre PC
 +
ps: dans Geany selectionner une ou plusieurs lignes et appuyer sur "Ctrl + E" pour commenter ou décommenter
 +
-->
<div class="body">
<div class="body">
 +
 +
 +
 +
 +
<center>
 +
<form method="get" >
 +
  <input type="button" value="< PREVIOUS <" onclick="document.location = '/Team:Grenoble/Projet/Modelling';" />
 +
  <select name="id" onchange="document.location = '/Team:Grenoble/Projet/Modelling' + this.options[this.selectedIndex].value ;">
 +
 +
    <optgroup label="Modelling Homepage">
 +
   
 +
    <option value="#Content" >Table of content</option>
 +
 +
    </optgroup>
 +
 +
    <optgroup label="Construction of the model" >
 +
                               
 +
                                    <option value="/Deterministic#Our_EquationsTS" selected="selected">Establishment of the equation - Toggle switch</option>
 +
 +
                                    <option value="/Deterministic#Our_EquationsQS" >Establishment of the equation - Quorum sensing</option>
 +
                               
 +
                                    <option value="/Deterministic#Our_algorithms" >Our algorithms</option>
 +
                               
 +
                                   
 +
                            </optgroup>
 +
                       
 +
                            <optgroup label="Stochastic Modelling">
 +
                               
 +
                                    <option value="/Stochastic#Geof">Sensitivity to noise</option>
 +
                               
 +
                                    <option value="/Stochastic#Gillespie_algorithm">Gillespie algorithm</option>
 +
                               
 +
                                    <option value="/Stochastic#Stats">Mean, standard deviation and stats</option>
 +
 +
                            </optgroup>
 +
 +
                            <optgroup label="Parameters">
 +
                           
 +
    <option value="/Parameters">Table of parameters</option>
 +
 +
    </optgroup>
 +
                    </select>
 +
                    <input type="hidden" name="id2" value="0" />
 +
                    <input type="submit" value="Go!" />
 +
  <input type="button" value="> NEXT >" onclick="document.location = '/Team:Grenoble/Projet/Modelling/Stochastic';" />
 +
               
 +
            </form>
 +
            </center>
 +
 +
<div class="left">
<div class="left">
-
    <h1>Modelling - Deterministic</h1>
+
    <div  class="blocbackground" id="Construction">
 +
    <h1>Construction of the model</h1>
     
     
-
      <a href="http://2011.iGEM.org/wiki/images/d/d1/Rapport_Equations.pdf">
+
      <a href="http://2011..org/wiki/images/d/d1/Rapport_Equations.pdf">
      <img src="http://2011.iGEM.org/wiki/skins/common/images/icons/fileicon-pdf.png" style="float: left; height: 20px; width: auto">
      <img src="http://2011.iGEM.org/wiki/skins/common/images/icons/fileicon-pdf.png" style="float: left; height: 20px; width: auto">
      PDF version of the next two sections (Equations for Toggle Switch and Quorum sensing)</a><br/>
      PDF version of the next two sections (Equations for Toggle Switch and Quorum sensing)</a><br/>
 +
<!--
      <div class="noindent"><p>You need MathML supported on your browser to read the equations on this page. However,
      <div class="noindent"><p>You need MathML supported on your browser to read the equations on this page. However,
      you can find these equations in the above PDF version.</p>
      you can find these equations in the above PDF version.</p>
      </div>
      </div>
 +
-->
       
       
-
     
+
<p> As a proof of concept, we will consider anhydrotetracycline (aTc) instead of Mercury in
-
<div  class="blocbackground" id="Our_EquationsTS">
+
our model, and the transcriptional regulator TetR in place of MerR. The TetR system is well
-
  <h2>Our equations and how we obtained them</h2>
+
characterized in E. coli, which facilitates the modelling. In addition, if the system works well
-
                  <h3>The Two levels of Modelling</h3>
+
with aTc, it should work as well with Mercury, Copper or lead for example.
 +
</p>
 +
<p>
 +
In addition, since aTc diffuse freely accross the membrane of the cell, we do not have to take
 +
complex uptake mechanisms into considerations. Mercury is ionized and its entry in the cells
 +
depends on the presence of transporter protein.<br/>
 +
So in the following chapter, we are going to use TetR instead of MerR and aTc instead of
 +
Mercury.
 +
</p>
 +
     
 +
    </div>
 +
<div  class="blocbackground" id="Two_level">
 +
                  <h2>The Two modules of Modelling</h2>
<p>
<p>
-
In order to facilitate the construction of the model, we divided the model into two levels :
+
Large-scale biochemical networks are classically decomposed into modules of smaller size to facilitate  
 +
the model building process and the model calibration. The approach consists in modelling each module
 +
separately and integrating the different models into a larger model of the whole system.
 +
Like divided our genetic network in severals part (see <a href="https://2011.igem.org/Team:Grenoble/Projet/Design">genetic network</a>),
 +
we also divided our model in two independant level of modelling:
<ul>
<ul>
-
                               <li>Toggle Switch modelling: to predict the state bacteria will be.</li>
+
                               <li><strong>The Toggle Switch module:</strong> modelling this network module allows to predict in
-
                               <li>Quorum Sensing and Coloration: to predict where the red line will appear on our device.</li>
+
                              which state the bacteria are. In particular, we can determine the switching conditions in bacteria
 +
                              and the localization of the switching area on the device (that depend on both IPTG and aTc
 +
                                concentrations). This gives indications on how to adjust the size of the device to improve the
 +
                                aTc detection.</li>
 +
                               <li><strong>The Quorum Sensing and Coloration module:</strong>the corresponding model is used to  
 +
                              predict the localization and the width of the red line on the device. The modelling results are
 +
                              used to improve the device precision, for instance, by choosing between a device with a continuous
 +
                              bacterial layer and a device with strips containing bacteria. Each strip has the same concentration
 +
                              of aTc, but a different IPTG concentration.</li>
</ul>
</ul>
</p>
</p>
<p>
<p>
-
The first level of the model will allow us to define the switch conditions in bacteria, depending on the concentrations of pollutant and IPTG.  
+
The first level of the model will allow us to define the switch conditions in bacteria, depending
-
From these results, we could see the switch zone on the device and therefore, the position of the red line. These results indicate how to resize our device to improve the detection.
+
on the concentrations of aTc and IPTG. From these results, we could see where the switch
 +
zone will appear on the device and therefore, the position of the red line. These parts of the
 +
results indicate the range of aTc that can be detected.
</p>
</p>
<p>
<p>
-
The second level will provide us with the red line width, an indicator of the system precision. From these results, we could improve the precision of our device, for instance,  
+
The second level will give us an estimation of the red line width, which indicates the system precision.
-
by choosing between a device with a continuous bacterial layer and a device with strips containing bacteria.  
+
Based on these results, we could improve the precision of our device, for instance, by comparing
-
Each strip has a different IPTG concentration, but the same concentration of Mercury.  
+
between a device with a continuous bacterial layer and a device with strips containing bacteria.
 +
Each strip has a different IPTG concentration, but the same concentration of Mercury.
</p>
</p>
-
<p>
+
-
As a proof of concept, we will consider anhydrotetracycline (aTc) instead of Mercury in our model,
+
<p><strong>Two independent levels of modelling which are coupled in order to get a
-
and the transcriptional regulator TetR in place of MerR. The TetR system is well characterized in <i>E. coli</i>,
+
<a href="https://2011.igem.org/Team:Grenoble/Projet/Results/Toggle#TS_QS">global simulation of the device.</a>
-
which facilitates the modelling. In addition, if the system works well with aTc, it should work as well with Mercury, Copper or lead for example.
+
</strong></p>
-
</p>
+
</div>
-
<p>
+
<div  class="blocbackground" id="Our_EquationsTS">
-
So in the following chapter, we are going to use TetR instead of MerR and aTc instead of Mercury.
+
    <h2>Establishment of the equation</h2>
-
</p>
+
-
 
+
  <h3>Toggle switch</h3>
  <h3>Toggle switch</h3>
 +
<p>In a first part, we define a model to caracterize the <a href="https://2011.igem.org/Team:Grenoble/Projet/Design/toggle">Toggle Switch module</a> of our genetic network.
 +
<br/></p>
 +
    <ol>
    <ol>
-
      <li>Biological Models</li>
+
      <li>Biological Model</li>
      <p>
      <p>
  A toggle switch consists of two genes, each coding for a protein
  A toggle switch consists of two genes, each coding for a protein
Line 61: Line 154:
      <p>
      <p>
  The biological system we are trying to implement is more complex,
  The biological system we are trying to implement is more complex,
-
  on both the biological and physical side. However, the toggle
+
  on both the biological and physical side. However, the toggle switch
-
  switch model is basically the same. In the study of the toggle
+
  model is basically the same. In the study of the toggle switch itself,
-
  switch itself, the system can be reduced to a simple two-state
+
  the system can be reduced to a simple two-state subsystem that we will
-
  subsystem that we will then use for the rest of our modelling. The
+
  then use for the rest of our modelling. However, our toggle switch model
 +
  is basically the same: we can reduce it to a simple two-state subsystem  
 +
  that we will then use for the rest of our modelling. The
  toggle switch itself is not influenced by the rest of the system,
  toggle switch itself is not influenced by the rest of the system,
  if we do not consider the RsmA regulatory system that will be
  if we do not consider the RsmA regulatory system that will be
Line 72: Line 167:
      </p>
      </p>
-
      <li>Mathematical Models</li>
+
      <li>Mathematical Model</li>
-
      <p>We use a common model for the toggle switch that we demonstrate
+
-
  below. The differential equation describing the production of TetR
+
-
  is as follows
+
-
      </p>
+
-
     
+
-
      <math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>TetR</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>k</mi>
+
-
    <mi>plac</mi>
+
-
      </msub>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>plac</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>plac</mi>
+
-
      </msub>
+
-
 
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>plac</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&;</mi>
+
-
<mi>TetR</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>TetR</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
 
+
-
 
+
-
     
+
-
     
+
      <p>
      <p>
-
For better understanding of this model we demonstrated it.
+
In order to get the state of the bacteria, we need to compute the concentration of both
-
The differential equation describing the production of xR is as follow :
+
repressors. To obtain these variations, we develop a system of ordinary differential equations (ODES)
 +
which governs the behavior of the Toggle Switch.
      </p>
      </p>
-
     
+
      <center>
-
      <math display="block">
+
      $      
-
      <mrow>
+
      \frac{d[TetR]}{dt} = \frac{k_{pLac}.[pLac]_{tot}}{1 +  (\frac{[lacI]}{K_{pLac} + \frac{K_{pLac}.[IPTG]}{K_{lacI-IPTG}}.})^\beta} - \delta_{TetR}.[TetR]$
-
<mfrac>
+
      <br/><br/>
-
  <mrow>
+
      $\frac{d[lacI]}{dt} = \frac{k_{pTet}.[pTet]_{tot}}{1 +  (\frac{[tetR]}{K_{pTet} + \frac{K_{pTet}.[aTc]}{K_{TetR-aTc}}.})^\gamma} - \delta_{lacI}.[lacI]$
-
    <mo>d</mo>
+
      </center>
-
    <mfenced open="[" close="]" separators=",">
+
-
      <mrow>
+
-
<mi>TetR</mi>
+
-
      </mrow>
+
-
    </mfenced>
+
-
  </mrow>
+
-
  <mrow>
+
-
    <mo>dt</mo>
+
-
  </mrow>
+
-
</mfrac>
+
-
<mo>=</mo>
+
-
<msub>
+
-
<mi>k</mi>
+
-
      <mi>plac</mi>
+
-
</msub>
+
-
<mfenced open="[" close="]" separators=",">
+
-
  <mrow>
+
-
    <msub>
+
-
    <mi>P</mi>
+
-
  <mi>lac free</mi>
+
-
    </msub>
+
-
  </mrow>
+
-
</mfenced>
+
-
<mo>-</mo>
+
-
<msub>
+
-
<mi>&delta;</mi>
+
-
      <mi>TetR</mi>
+
-
</msub>
+
-
<mfenced open="[" close="]" separators=",">
+
-
  <mrow>
+
-
    <mi>TetR</mi>
+
-
  </mrow>
+
-
</mfenced>
+
-
      </mrow>
+
-
      </math>
+
-
 
+
      <p>
      <p>
-
with [Plac free ] being the concentration of available binding sites - i.e. not repressed by LacI molecule.
+
With this ODE system, we follow the evolution of the concentration of the two toggle switch repressors,
-
Plac_free is of course related to the total number of promoters Plac :
+
TetR and LacI. This gives us the state of the bacteria. A demonstration of this ODE system is available
-
 
+
in the previous pdf file. We briefly explain the equations below.
-
     
+
  </p>
-
      <math display="block">
+
  <p>
-
      <mrow>
+
Both equations are developed following the same approach. There is a term of production and a term of
-
<mfenced open="[" close="]" separators=",">
+
degradation. The parameters $k_{pLac}.[pLac]_{tot}$ represent the protein synthesis rate from the pLac promoter.
-
  <mrow>
+
K_{pLac} and K_{lacI−IPTG} are the dissociation constants of LacI and pLac, and LacI and IPTG, respectively.
-
    <msub>
+
The parameters β and γ denote the cooperativity of repression, that is, the number of repressors bound
-
  <mrow>
+
to the promoter.  
-
    <mi>P</mi>
+
  </p>
-
  </mrow>
+
  <p>
-
  <mi>lac free</mi>
+
According to these equations, the rate of variation of repressor TetR is inhibited by the repressor LacI.
-
    </msub>
+
The degree of inhibition is modulated by the IPTG concentration. Reciprocally in the second equation,  
-
  </mrow>
+
the rate of variation of LacI depends on TetR, whose negative effect is modulated by aTc.
-
</mfenced>
+
  </p>
-
<mo>+</mo>
+
  <p><strong>
-
<mfenced open="[" close="]" separators=",">
+
This indicates that the two equations are coupled. And also that only one repressor could be
-
  <mrow>
+
predominant, as shown later.
-
    <msub>
+
  </strong></p>
-
    <mi>P</mi>
+
    </p>
-
  <mi>lac - LacI</mi>
+
-
    </msub>
+
-
  </mrow>
+
-
</mfenced>
+
-
<mo>=</mo>
+
-
<mfenced open="[" close="]" separators=",">
+
-
  <mrow>
+
-
    <msub>
+
-
    <mi>P</mi>
+
-
  <mi>lac total</mi>
+
-
    </msub>
+
-
  </mrow>
+
-
</mfenced>
+
-
      </mrow>
+
-
      </math>
+
-
     
+
-
     
+
-
with [Plac − LacI ] being the concentration of promoters repressed by LacI. If we set
+
-
<math >
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>plac</mi>
+
-
  </msub>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac free</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
 
+
-
      <mi>LacI</mi>
+
-
 
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac - LacI</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
we get :
+
-
 
+
-
<math display="block">
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>P</mi>
+
-
<mrow>
+
-
    <mi>lac free</mi>
+
-
      </msub>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>LacI</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>plac</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
 
+
-
  We then try to get [LacI] :
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>LacI - IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>LacI</mi>
+
-
<mi>free</mi>
+
-
      </msub>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>LacI - plac</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>=</mo>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
     
+
-
      <mi>LacI</mi>
+
-
   
+
-
     
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
with [LacI - IPTG] the concentration of LacI bound to IPTG and [LacI - plac ] the concentration of the complex of
+
-
LacI and the promoter. If we set
+
-
<math >
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>IPTG</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI - IPTG</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
we get :
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>LacI</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>LacI</mi>
+
-
<mi>total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
+
-
which finally gives our differential equations for TetR :
+
-
      <math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>TetR</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>k</mi>
+
-
    <mi>plac</mi>
+
-
      </msub>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>plac</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>plac</mi>
+
-
      </msub>
+
-
 
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>plac</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>TetR</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>TetR</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
<p>
<p>
-
  The equation can be generalized to account for cooperativity arising from
+
  These two equations can be easily computed with a differential solver. We can precisely estimate the effects of each parameter.
-
  multimerization of the transcription factors, here represented by
+
-
  the cooperativity constant n<SUB>plac</SUB>
+
-
<p>
+
-
+
-
In a  similar way, we obtain a differential equation for LacI:
+
-
+
-
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>k</mi>
+
-
    <mi>pTet</mi>
+
-
      </msub>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>Tet total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>TetR</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>pTet</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <msub>
+
-
    <mi>K</mi>
+
-
    <mi>pTet</mi>
+
-
  </msub>
+
-
     
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>aTc</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>TetR - aTc</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>pTet</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>LacI</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>LacI</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
</p>
+
-
 
+
-
  These two equations can be easily computed with a differential solver. We can precisely estimate the effects of each parameter.
+
-
 
+
</p>
</p>
    </ol>
    </ol>
 +
    <p>
 +
With this model, we were able to predict the <a href="https://2011.igem.org/Team:Grenoble/Projet/Results/Toggle#TS_QS">behavior of our toggle switch</a>.
 +
    </p>
</div>
</div>
<div  class="blocbackground" id="Our_EquationsQS">
<div  class="blocbackground" id="Our_EquationsQS">
-
  <h2>Our equations and how we obtained them</h2>  
+
  <h2>Establishment of the equation</h2>  
  <h3>Quorum sensing</h3>
  <h3>Quorum sensing</h3>
    <ol>
    <ol>
-
      <li>Mathematical Models</li>
+
      <li>Mathematical Model</li>
      <p>
      <p>
-
Our work mainly refers to the models set up by the 2007 iGEM Bangalore team. On the basis of their work we set
+
In a second part, we define a model able to characterize the <a href="https://2011.igem.org/Team:Grenoble/Projet/Design/quorum">quorum sensing module</a> of our genetic network,
-
up models adapted to our own system. For these reasons we strongly recommend getting familiar with the works
+
which involves the quorum sensing genes CinI and CinR, as well as the signaling molecule AHL.<br/>
-
of the 2007 Bangalore team for an easier understanding of the models we used.<br/>
+
-
The main difference between our models is that their model is designed for a whole medium, in which the concen-
+
In order to model the Quorum Sensing module, we detail below the different reactions taking place
-
trations of quorum sensing molecules are considered for a whole fixed volume of a medium. Our system, however, is
+
inside this module. For reasons that will become clear later, we focus on a particular area of our
-
supposed to describe the spatial diffusion of quorum sensing molecules as well, and therefore needs to be designed
+
device, where neighboring bacteria will have a different behavior, although they carry the same
-
for an infinitesimal volume of medium containing bacteries and outside medium.
+
genetic circuit.
-
A few other differences exist between our model and theirs, mainly due to the fact that the system we intend to
+
  </p>
-
describe is made of other different parts. For example the production rate of our Quorum Sensing enzymes are
+
  <img src="https://static.igem.org/mediawiki/2011/a/a5/QS_details_2.png" class="centerwide" style="bow-shadow: non"/>
-
directly linked to the previously described toggle switch model.
+
  <div class="legend"><strong>Figure 1:</strong>Mechanism of Quorum Sensing diffusion at the boundary</div>
-
      </p>
+
  <p>
-
      <p>
+
According to the figure, several  must be taken into account:
-
For these reasons we strongly recommend getting familiar with the works of the 2007 Bangalore team for an
+
<ol>
-
easier understanding of the models we used.
+
<li>the production of the Quorum Sensing molecule</li>
-
      </p>
+
<li>the secretion of the molecule</li>
-
      <p>
+
<li>the diffusion of the molecule in the medium</li>
-
Bangalore 07 modeled the behaviour of quorum sensing for a simple quorum sensing system. With the input of
+
<li>the penetration of the molecule</li>
-
the toggle switch model taken into account, we can adapt their equations to our system. With our toggle switch system the production would be ruled by the regulatory network of LacI and TetR :
+
<li>the complexation of the molecule with its receptor</li>
-
      </p>
+
<li>the activation of the coloration</li>
-
      <math display="block">
+
</ol>
-
<mrow>
+
  </p>
-
  <mfrac>
+
  <p>
-
    <mrow>
+
To model these mecanisms, we need to follow the evolution of the following quantities
-
      <mo>d</mo>
+
<ul>
-
      <mfenced open="[" close="]" separators=",">
+
<li>$[QS_i]$ concentration of the intracellular Quorum Sensing molecule.</li>
-
<mrow>
+
<li>$[QS_e]$ concentration of the extracellular Quorum Sensing molecule.</li>
-
  <mi>CinI</mi>
+
<li>$[cinR]$ concentration of the Quorum Sensing receptor.</li>
-
</mrow>
+
<li>$[cinI]$ concentration of the Quorum Sensing producer enzyme.</li>
-
      </mfenced>
+
<li>$[cinR_{comp}]$ concentration of the complexe cinR-QS.</li>
-
    </mrow>
+
</ul>
-
    <mrow>
+
  </p>
-
      <mo>dt</mo>
+
  <p>
-
    </mrow>
+
Based on the Bangalore 2007 iGEM team, we get the following system of equations:
-
  </mfrac>
+
  </p>
-
  <mo>=</mo>
+
  <center>
-
    <mfrac>
+
  $\frac{d[QS_i]}{dt} = \eta([QS_e]-[QS_i])-\delta_{QSi} [QS_i] + k_{QS-production}'[cinI]$<br/><br/>
-
    <mrow>
+
  $\frac{d[QS_e]}{dt} = \rho v_c\eta([QS_i]-[QS_e])-\delta_{QSe} [QS_e] + D_{diff}\frac{\partial^2 [QS_e]}{\partial x^2}$<br/><br/>
-
      <msub>
+
  $\frac{d[cinR_{free}]}{dt} = \frac{k_{pLac}.[pLac]_{tot}}{1 +  (\frac{[lacI_{total}]}{K_{pLac} + \frac{K_{pLac}.[IPTG]}{K_{lacI-IPTG}}.})^\beta} - \delta_{cinR}[cinR_{free}] - V_{complexation}$<br/><br/>
-
      <mi>k</mi>
+
  $\frac{d[cinR_{comp}]}{dt} = K_{comp}([cinR_{free}].[QS_i])$<br/><br/>
-
    <mi>pTet</mi>
+
  </center>
-
      </msub>
+
  <p>
-
      <mfenced open="[" close="]" separators=",">
+
In the first equation, expressing the evolution of the concentration of the intracellular Quorum Sensing
-
<mrow>
+
molecule, 3 terms are involved: $[QSe]−[QSi]$, which describes the diffusion through the membrane,  
-
  <msub>
+
$\delta_{QSi}[QSi]$, the degradation and $k_{QS−production}[cinI]$, the production of Quorum Sensing molecule
-
  <mi>P</mi>
+
by the enzyme CinI.
-
<mi>Tet total</mi>
+
In the second equation, expressing the evolution of extracellular Quorum Sensing, there is no production term, but a spatial diffusion term
-
  </msub>
+
$D_{diff}\frac{\partial^2 [QS_e]}{\partial x^2}$.
-
</mrow>
+
  </p>
-
      </mfenced>
+
  <p>
-
    </mrow>
+
The concentrations of CinI and CinR can be obtained by using the toggle switch modelling. Indeed, since CinI
-
    <mrow>
+
is on the pathway of LacI and CinR on the pathway of Tet, their evolution follow the same equations.
-
      <mi>1 +</mi>
+
In addition we consider the complexation of the CinR protein and the Quorum Sensing molecule,
-
      <msup>
+
which is expressed by the term $V_{complexation}$ in the CinR equation:
-
    <mrow>
+
\[V_{complexation} = K_{comp}[QS_i][CinR_{free}]\]
-
      <mfenced open="(" close=")" separators=",">
+
with $K_{comp}$ the affinity constant of AHL for cinR.
-
<mrow>
+
  </p>
-
  <mfrac>
+
  <p>
-
    <mrow>
+
In order to simplify the model, we considered that the complexation of CinR to AHL is total and depends only
-
      <mfenced open="[" close="]" separators=",">
+
on $[cinR]$ and $[QS_i] which is the limitant factor$.
-
<mrow>
+
  </p>
-
  <mi>TetR</mi>
+
  <p><strong>
-
</mrow>
+
To solve this set of equations, we couldn't use a classical ODE solver from Matlab (Mathworks), because
-
      </mfenced>
+
the equations are derived both in time and space. We therefore needed to use the finite difference method.
-
    </mrow>
+
To that aim, we build a matrix based on Taylor's series discretization.
-
    <mrow>
+
  </strong></p>
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>pTet</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <msub>
+
-
    <mi>K</mi>
+
-
    <mi>pTet</mi>
+
-
  </msub>
+
-
     
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>aTc</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>TetR - aTc</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>pTet</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
 
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>CinI</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>CinI</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
     
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
    <mi>CinR</mi>
+
-
    <mi>free</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>k</mi>
+
-
    <mi>plac</mi>
+
-
      </msub>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>plac</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>plac</mi>
+
-
      </msub>
+
-
 
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>plac</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
 
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>CinR</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
  <msub>
+
-
    <mi>CinR</mi>
+
-
    <mi>free</mi>
+
-
  </msub>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
    <msub>
+
-
    <mi>V</mi>
+
-
  <mi>complexation</mi>
+
-
    </msub>
+
-
</mrow>
+
-
</math>
+
<p>
<p>
-
  We can therefore describe the production of CinI and CinR<SUB>free</SUB> inside the cells. V<SUB>complexation</SUB>
+
<li>Definition of the matrix</li>
-
  is the complexation rate of CinR<SUB>free</SUB> with AHL molecule. As a matter of fact CinR will be transformed into
+
-
  CinR* after being complexed with the Quorum Sensing molecules entering the cell. It is now taken into account via this
+
-
  complexation rate.<br/>
+
-
  A simple way to write this rate would be as follow :
+
-
+
-
<math display="block">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>V</mi>
+
-
<mi>complexation</mi>
+
-
  </msub>
+
-
  <mo>=</mo>
+
-
  <msub>
+
-
  <mi>k</mi>
+
-
<mi>comp</mi>
+
-
  </msub>
+
-
  <msubsup>
+
-
  <mi>Q</mi>
+
-
<mi>i</mi>
+
-
<mi>n</mi>
+
-
  </msubsup>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
  <msub>
+
-
    <mi>CinR</mi>
+
-
    <mi>free</mi>
+
-
  </msub>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
with Qi being the concentration in QS molecule inside the cell. If we consider that only one QS molecule would
+
-
bind to a CinR molecule, we obtain the following equation for CinR :
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
    <mi>CinR</mi>
+
-
    <mi>free</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>k</mi>
+
-
    <mi>plac</mi>
+
-
      </msub>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>P</mi>
+
-
<mi>lac total</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>plac</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>CinR</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
  <msub>
+
-
    <mi>CinR</mi>
+
-
    <mi>free</mi>
+
-
  </msub>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
    <msub>
+
-
  <mi>k</mi>
+
-
<mi>comp</mi>
+
-
  </msub>
+
-
  <msubsup>
+
-
  <mi>Q</mi>
+
-
<mi>i</mi>
+
-
<mi></mi>
+
-
  </msubsup>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
  <msub>
+
-
    <mi>CinR</mi>
+
-
    <mi>free</mi>
+
-
  </msub>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
+
-
</p>
+
<p>
<p>
-
  For the following equations the physical volume considered is an infinitesimal volume of medium along x - i.e. we
+
To solve this set of equations we have to use a matrix that will describe our system in both space
-
  only consider an l ∗ dx volume of cell, l being the width of our plate and dx an infinitesimal portion of length.
+
and time. for example for the QS molecule outside of the cell :
-
  In this infinitesimal volume we set a fixed number of non-growing cells and take into account the diffusion from
+
-
  one portion to the next ones.
+
-
</p>
+
-
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qi</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mi>&eta;</mi>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qe</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
      <mo>-</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qi</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>Qi</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>Qi</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <mi>f([CinI])</mi>
+
-
</mrow>
+
-
</math>
+
-
+
-
<math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qe</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mi>&rho;</mi>
+
-
  <msub>
+
-
      <mi>v</mi>
+
-
      <mi>c</mi>
+
-
  </msub>
+
-
  <mi>&eta;</mi>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qi</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
      <mo>-</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qe</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>Qe</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>Qe</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <msub>
+
-
  <mi>D</mi>
+
-
<mi>diff</mi>
+
-
  </msub>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <msup>
+
-
      <mo>&PartialD;</mo>
+
-
    <mn>2</mn>
+
-
      </msup>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qe</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>&PartialD;</mo>
+
-
      <msup>
+
-
      <mi>x</mi>
+
-
    <mn>2</mn>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
+
-
<ul>
+
-
  <li>With f ([CinI]) being a mathematical function describing the production of QS molecule by CinI enzyme.
+
-
      Basically this fonction would be as follow :</li>
+
-
  <math display="block">
+
-
  <mrow>
+
-
    <mi>f([CinI]) =</mi>
+
-
    <msub>
+
-
    <mi>k</mi>
+
-
  <msub>
+
-
  <mi>QS</mi>
+
-
<mi>p</mi>
+
-
  </msub>
+
-
    </msub>
+
-
    <msup>
+
-
  <mrow>
+
-
    <mfenced open="[" close="]" separators=",">
+
-
      <mrow>
+
-
<mi>substrate</mi>
+
-
      </mrow>
+
-
    </mfenced>
+
-
  </mrow>
+
-
  <mi>n</mi>
+
-
    </msup>
+
-
    <mfenced open="[" close="]" separators=",">
+
-
      <mrow>
+
-
<mi>CinI</mi>
+
-
      </mrow>
+
-
    </mfenced>
+
-
  </mrow>
+
-
  </math>
+
-
  But if this reaction is assumed first-order, we obtain :
+
-
 
+
-
  <math display="block">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mo>d</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qi</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mo>dt</mo>
+
-
    </mrow>
+
-
  </mfrac>
+
-
  <mo>=</mo>
+
-
  <mi>&eta;</mi>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qe</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
      <mo>-</mo>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>Qi</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<mi>Qi</mi>
+
-
  </msub>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>Qi</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <msubsup>
+
-
  <mi>k</mi>
+
-
<msub>
+
-
<mi>QS</mi>
+
-
      <mi>p</mi>
+
-
</msub>
+
-
<mi>'</mi>
+
-
  </msubsup>
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>CinI</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
+
-
<li>
+
-
  With Ddiff being the diffusion coefficient for our Quorum sensing molecule in our medium along spatial
+
-
  dimension x.
+
-
</li>
+
-
<li>
+
-
  In our case ρvc is a constant (we consider the cells do not grow in our time scale)
+
-
</li>
+
</p>
</p>
 +
<center>
 +
$M_{QSe}(m,n) = [QS_e](x,t)$<br/>
 +
$M_{QSe}(m+1,n+1) = [QS_e](x + dx,t+dt)$
 +
</center>
<p>
<p>
-
  With the equations set (3.1); (3.3); (3.5); (3.6) we have, we can not use solvers like matlab ODE because of
+
In these equations, m represents the spatial dimension and n the temporal dimension.
-
  their space and time dependancies. To solve our problem we have to use a space-time derivation matrix we will
+
-
  describe in the next chapter.
+
</p>
</p>
-
 
-
</ul>
 
-
 
-
<li>
 
-
  Solvation ot the set of equations (3.1); (3.3); (3.5); (3.6)
 
-
<li>
 
-
<p>
 
-
    To solve this set of equations we have to use a matrix that will describe our system in both space and time. for
 
-
    example for the QS molecule outside of the cell :
 
-
</p>
 
-
<math display="block">
 
-
<mrow>
 
-
  <msub>
 
-
  <mi>M</mi>
 
-
<msub>
 
-
<mi>Q</mi>
 
-
      <mi>e</mi>
 
-
</msub>
 
-
  </msub>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>m,n</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
  <mo>=</mo>
 
-
  <mfenced open="[" close="]" separators=",">
 
-
    <mrow>
 
-
      <msub>
 
-
      <mi>Q</mi>
 
-
    <mi>e</mi>
 
-
      </msub>
 
-
    </mrow>
 
-
  </mfenced>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>x,t</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
</mrow>
 
-
</math>
 
-
 
-
<math display="block">
 
-
<mrow>
 
-
  <msub>
 
-
  <mi>M</mi>
 
-
<msub>
 
-
<mi>Q</mi>
 
-
      <mi>e</mi>
 
-
</msub>
 
-
  </msub>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>m+1,n+1</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
  <mo>=</mo>
 
-
  <mfenced open="[" close="]" separators=",">
 
-
    <mrow>
 
-
      <msub>
 
-
      <mi>Q</mi>
 
-
    <mi>e</mi>
 
-
      </msub>
 
-
    </mrow>
 
-
  </mfenced>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>x+dx,t+dt</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
</mrow>
 
-
</math>
 
<img src="http://2011.iGEM.org/wiki/images/c/c6/Matrix_QS.png" class="centerwide" style="box-shadow: none"/>
<img src="http://2011.iGEM.org/wiki/images/c/c6/Matrix_QS.png" class="centerwide" style="box-shadow: none"/>
<ul>
<ul>
Line 1,362: Line 313:
  </li>
  </li>
  <li>
  <li>
-
    Of course, Qi, CinI and CinR matrices will be similarly implemented.
+
    Of course, QSi, CinI and CinR matrices will be similarly implemented.
  </li>
  </li>
</ul>
</ul>
 +
 +
<li>Discretization of the equation</li>
<p>
<p>
-
  With our continuous equations set, we want to obtain discrete definition of each of the matrices. The interdepen-
+
  With our continuous equations set, we want to obtain discrete definition of each of the matrices. interdependencies
-
  dancies of the equations imply that the computation of the matrices will be performed on the entire CinI matrix
+
  of the equations imply that the computation of the matrices will be performed on the entire CinI matrix
-
  first, then each line of the Qi and Qe matrices will be computed alternatively. Finally CinR matrix computation
+
  first, then each line of the Qi and Qe matrices will be computed alternatively. The computation of the CinR
-
  will be performed.
+
  will be eventually performed.
</p>
</p>
<p>
<p>
Line 1,376: Line 329:
  Discretization is obtained with first order taylor series :
  Discretization is obtained with first order taylor series :
</p>
</p>
-
<math display="block">
+
</ol>
-
<mrow>
+
<center>
-
  <msub>
+
$
-
  <mi>M</mi>
+
M_{QSi}(m,n+1) =\Delta t (\eta (M_{QSe}(m,n) -  M_{QSi}(m,n)) - \delta_{QSi}.M_{QSi}(m,n) + k_{QSp}M_{CinI}(m,n)) + M_{QSi}(m,n)
-
<msub>
+
$<br/><br/>
-
<mi>Q</mi>
+
$
-
      <mi>i</mi>
+
M_{QSe}(m,n+1) =\Delta t ( D_{m} + D_{diff} \frac{M_{QSe}(m+1,n) - 2 M_{QSe}(m,n) + M_{QSe}(m-1,n)}{\Delta x^2}) + M_{QSe}(m,n)
-
</msub>
+
$<br/><br/>
-
  </msub>
+
$
-
  <mfenced open="(" close=")" separators=",">
+
with D_{m} =\rho v_c \eta .M_{QSi}(m,n) - M_{QSe}(m,n)(\delta_{QSe} + \rho v_c \eta)
-
    <mrow>
+
$<br/><br/>
-
      <mi>m,n+1</mi>
+
$
-
    </mrow>
+
M_{CinR_{free}}(m,n+1) = \Delta t (\frac{k_{pTet}[P_{Tet total}]}{1+ (\frac{[TetR]}{K_{pTet}(1+\frac{[aTc]}{K_{TetR - aTc}})})^{n_{pTet}}} - M_{CinR_{free}}(m,n)(\delta_{CinR} - k_{comp}.M_{Qi}(m,n))) + M_{CinR_{free}}(m,n)$<br/>
-
  </mfenced>
+
</center>
-
  <mo>=</mo>
+
-
  <mi>&Delta;</mi>
+
-
  <mi>t</mi>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>&eta;</mi>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mi>(m,n)</mi>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>i</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>&delta;</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>i</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>i</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <msub>
+
-
  <mi>k</mi>
+
-
<msub>
+
-
<mi>QS</mi>
+
-
      <mi>p</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<mi>CinI</mi>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
 
+
-
  <mo>+</mo>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>i</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
 
+
-
</mrow>
+
-
     
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
<math display="block">
+
<p><strong>
-
<mrow>
+
With these discrete equations the 4 matrices can be computed through simple calculation loops over each line.
-
  <msub>
+
The CinI matrix does not depend on space dimension, it is then possible to compute it without discretization with
-
  <mi>M</mi>
+
a differential solver.</strong>
-
<msub>
+
</p>
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n+1</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>=</mo>
+
-
  <mi>&Delta;</mi>
+
-
  <mi>t</mi>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>D</mi>
+
-
    <mi>m</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <msub>
+
-
      <mi>D</mi>
+
-
    <mi>diff</mi>
+
-
      </msub>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m+1,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>2M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>+</mo>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m-1,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <mspace />
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
-
<p>with
+
<p><strong>
-
<math >
+
Moreover to get the coupling of toggle switch and quorum sensing modules, we used the results of the first one
-
<mrow>
+
(lacI and TetR evolution) to get the evolution of quorum sensing proteins (respectively cinI and cinR).
-
  <msub>
+
It means that the output of the first module are used as input for the second module.</strong>
-
  <mi>D</mi>
+
-
<mi>m</mi>
+
-
  </msub>
+
-
  <mo>=</mo>
+
-
  <mi>&rho;</mi>
+
-
  <msub>
+
-
  <mi>v</mi>
+
-
<mi>c</mi>
+
-
  </msub>
+
-
  <mi>&eta;</mi>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>i</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mo>-</mo>
+
-
  <msub>
+
-
  <mi>M</mi>
+
-
<msub>
+
-
<mi>Q</mi>
+
-
      <mi>e</mi>
+
-
</msub>
+
-
  </msub>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <mi>m,n</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
  <mfenced open="(" close=")" separators=",">
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>&delta;</mi>
+
-
    <msub>
+
-
    <mi>Q</mi>
+
-
  <mi>e</mi>
+
-
    </msub>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mi>&rho;</mi>
+
-
      <msub>
+
-
      <mi>v</mi>
+
-
    <mi>c</mi>
+
-
      </msub>
+
-
      <mi>&eta;</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
</math>
+
</p>
</p>
-
 
-
<math display="block">
 
-
<mrow>
 
-
  <msub>
 
-
  <mi>M</mi>
 
-
<mi>CinR</mi>
 
-
  </msub>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>m,n+1</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
  <mo>=</mo>
 
-
  <mi>&Delta;</mi>
 
-
  <mi>t</mi>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
  <mfrac>
 
-
    <mrow>
 
-
      <msub>
 
-
      <mi>k</mi>
 
-
    <mi>plac</mi>
 
-
      </msub>
 
-
      <mfenced open="[" close="]" separators=",">
 
-
<mrow>
 
-
  <msub>
 
-
  <mi>P</mi>
 
-
<mi>lac total</mi>
 
-
  </msub>
 
-
</mrow>
 
-
      </mfenced>
 
-
    </mrow>
 
-
    <mrow>
 
-
      <mi>1 +</mi>
 
-
      <msup>
 
-
    <mrow>
 
-
      <mfenced open="(" close=")" separators=",">
 
-
<mrow>
 
-
  <mfrac>
 
-
    <mrow>
 
-
      <mfenced open="[" close="]" separators=",">
 
-
<mrow>
 
-
  <mi>LacI</mi>
 
-
</mrow>
 
-
      </mfenced>
 
-
    </mrow>
 
-
    <mrow>
 
-
      <msub>
 
-
<mi>K</mi>
 
-
<mi>plac</mi>
 
-
      </msub>
 
-
      <mo>+</mo>
 
-
      <mfrac>
 
-
<mrow>
 
-
      <msub>
 
-
<mi>K</mi>
 
-
<mi>plac</mi>
 
-
      </msub>
 
-
 
-
  <mfenced open="[" close="]" separators=",">
 
-
    <mrow>
 
-
      <mi>IPTG</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
</mrow>
 
-
<mrow>
 
-
  <msub>
 
-
  <mi>K</mi>
 
-
<mi>LacI - IPTG</mi>
 
-
  </msub>
 
-
</mrow>
 
-
      </mfrac>
 
-
    </mrow>
 
-
  </mfrac>
 
-
</mrow>
 
-
      </mfenced>
 
-
    </mrow>
 
-
    <msub>
 
-
    <mi>n</mi>
 
-
  <mi>plac</mi>
 
-
    </msub>
 
-
      </msup>
 
-
    </mrow>
 
-
  </mfrac>
 
-
      <mo>-</mo>
 
-
      <msub>
 
-
      <mi>M</mi>
 
-
    <mi>CinR</mi>
 
-
      </msub>
 
-
      <mfenced open="(" close=")" separators=",">
 
-
<mrow>
 
-
  <mi>m,n</mi>
 
-
</mrow>
 
-
      </mfenced>
 
-
      <mfenced open="(" close=")" separators=",">
 
-
<mrow>
 
-
  <msub>
 
-
  <mi>&delta;</mi>
 
-
<mi>CinR</mi>
 
-
  </msub>
 
-
  <mo>-</mo>
 
-
  <msub>
 
-
  <mi>k</mi>
 
-
<mi>comp</mi>
 
-
  </msub>
 
-
  <msub>
 
-
  <mi>M</mi>
 
-
<msub>
 
-
<mi>Q</mi>
 
-
      <mi>i</mi>
 
-
</msub>
 
-
  </msub>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>m,n</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
</mrow>
 
-
      </mfenced>
 
-
    </mrow>
 
-
  </mfenced>
 
-
  <mo>+</mo>
 
-
  <msub>
 
-
  <mi>M</mi>
 
-
<mi>CinR</mi>
 
-
  </msub>
 
-
  <mfenced open="(" close=")" separators=",">
 
-
    <mrow>
 
-
      <mi>m,n</mi>
 
-
    </mrow>
 
-
  </mfenced>
 
-
</mrow>
 
-
</math>
 
-
 
-
 
-
 
-
 
-
</ol>
 
<p>
<p>
-
With these discrete equations the 4 matrices can be computed through simple calculation loops over each line.
+
With this model, we were able to predict how the <a href="https://2011.igem.org/Team:Grenoble/Projet/Results/Toggle#QS">red stripe appears</a> on the plate
-
The CinI matrix does not depend on space dimension, it is then possible to compute it without discretization with
+
-
a differential solver.
+
</p>
</p>
Line 1,781: Line 367:
  <h2>Our algorithms</h2>
  <h2>Our algorithms</h2>
    <p>
    <p>
-
      In the MATLAB archive that can be found <a href="http://iGEMgrenoble-files.perso.sfr.fr/2011/MATLAB_Archives/">here</a>
+
      An archive containing our Matlab scripts for the deterministic modeling can be found <a href="http://iGEMgrenoble-files.perso.sfr.fr/2011/MATLAB_Archives/">here</a>
-
      containing our matlab scripts for deterministic modelling (file Deterministic_archive.tar.gz) you can launch an ODE based
+
      (file Deterministic_archive.tar.gz). You can launch and ODE-based simulation(see our ODEs in  
-
      simulation (see our ODEs in the two previous sections) with the file biosenseur1Dmain.m.
+
      the two previous sections) with the file biosenseur1Dmain.m.
    </p>
    </p>
    <p>
    <p>
-
      Several dialog boxes will pop up to enter the specificities of the simulation : (physical  
+
      Several dialog boxes will pop up to enter the specificities of the simulation: (physical  
-
      specificities of the device, chemical species concentrations and IPTG gradient )
+
      specificities of the device, chemical species concentrations and IPTG gradient).
    </p>
    </p>
     
     
    <p>
    <p>
-
      At the end of the simulation you obtain 3 matrices named M_stock, M_QS and M_comp containing the concentrations in each protein
+
At the end of the simulation you obtain 3 matrices named M_stock, M_QS and M_comp containing the concentrations
-
      species at each time point and on each physical point of the plate. We wrote three MATLAB scripts that display the concentration in proteins
+
in each protein species at each time point and on each physical point of the plate. We wrote three Matlab scripts
-
      dynamically that you can call with DynamicplottingTS, DynamicplottingQS and DynamicplottingCP. For a good understanding of the models and
+
(DynamicplottingTS, DynamicplottingQS and DynamicplottingCP) that dynamically display the protein concentrations.
-
      of our results we also wrote a script to illustrate the coloration of our plate through time according to our models named Imageshow.m.
+
For a good understanding of the models and of our results, we also wrote a script (Imageshow.m) to illustrate
-
    </p>
+
the plate coloration.
-
   
+
</p>
-
+
-
</div>
+
-
<div  class="blocbackground" id="Isoclines_and_Hysteresis">
+
-
  <h2>Nullclines and Hysteresis</h2>
+
-
    <p>
+
-
In order to predict the stability of our system, mathematical studies are necessary.
+
-
    </p>
+
-
    <h3>Nullclines</h3>
+
-
<p>
+
-
In a first time, an isocline study is realized.
+
-
</p>
+
-
<p>
+
-
Nullclines are a classical tool to determine the stationary point(s) of a system. They are obtained by setting to zero the time-derivative of each variable.
+
-
For instance in our model, d[TetR]/dt=0 allows us to determine the nullcline of [TetR] as a function of [LacI]. d[LacI]/dt=0 allows us to determine the nullcline of [LacI] as a function of [TetR]
+
-
The intersection point of all the nullclines is a stationary point of the system, when the rate of change of the repressor concentrations are equal to zero.
+
-
</p>
+
-
<img src="https://static.igem.org/mediawiki/2011/5/57/System_diff.png" class="centerwide" style="box-shadow: none"/>
+
-
   
+
-
<p>
+
-
To facilitate the manipulation of the equations and reduce the number of parameters, we introduce new parameters and concentration variables:
+
-
</p>
+
-
<ul>
+
-
<li>
+
-
E_TetR = kplac * [pLac total]
+
-
</li>
+
-
<li>
+
-
<math display="block">
+
-
<mrow>
+
-
    <mrow>
+
-
      <mo>RtetR</mo>
+
-
    </mrow>
+
-
  <mo>=</mo>
+
-
    <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>1</mi>
+
-
    <mi></mi>
+
-
      </msub>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>TetR</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>pTet</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <msub>
+
-
    <mi>K</mi>
+
-
    <mi>pTet</mi>
+
-
  </msub>
+
-
     
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>aTc</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>TetR - aTc</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>pTet</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</math>
+
-
</li>
+
-
<li>
+
-
E_LacI = kpTet * [pTet total]
+
-
</li>
+
-
<li>
+
-
<math display="block">
+
-
<mrow>
+
-
    <mrow>
+
-
      <mo>RLacI</mo>
+
-
    </mrow>
+
-
  <mo>=</mo>
+
-
    <mfrac>
+
-
    <mrow>
+
-
      <msub>
+
-
      <mi>1</mi>
+
-
    <mi></mi>
+
-
      </msub>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <mi>1 +</mi>
+
-
      <msup>
+
-
    <mrow>
+
-
      <mfenced open="(" close=")" separators=",">
+
-
<mrow>
+
-
  <mfrac>
+
-
    <mrow>
+
-
      <mfenced open="[" close="]" separators=",">
+
-
<mrow>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <mrow>
+
-
      <msub>
+
-
<mi>K</mi>
+
-
<mi>pLac</mi>
+
-
      </msub>
+
-
      <mo>+</mo>
+
-
      <mfrac>
+
-
<mrow>
+
-
  <msub>
+
-
    <mi>K</mi>
+
-
    <mi>pLac</mi>
+
-
  </msub>
+
-
     
+
-
  <mfenced open="[" close="]" separators=",">
+
-
    <mrow>
+
-
      <mi>IPTG</mi>
+
-
    </mrow>
+
-
  </mfenced>
+
-
</mrow>
+
-
<mrow>
+
-
  <msub>
+
-
  <mi>K</mi>
+
-
<mi>LacI - IPTG</mi>
+
-
  </msub>
+
-
</mrow>
+
-
      </mfrac>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
      </mfenced>
+
-
    </mrow>
+
-
    <msub>
+
-
    <mi>n</mi>
+
-
  <mi>pLac</mi>
+
-
    </msub>
+
-
      </msup>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</math>
+
-
</li>
+
-
<li>
+
-
[TetR]r = RTetR * [TetR] the relative concentration of TetR
+
-
</li>
+
-
<li>
+
-
[LacI]r = RLacI * [LacI] the relative concentration of LacI
+
-
</li>
+
-
<li>
+
-
<math >
+
-
<mrow>
+
-
  <mrow>
+
-
  <mo>K</mo>
+
-
  </mrow>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
<mrow>
+
-
  <mi>RtetR *</mi>
+
-
</mrow>
+
-
<mrow>
+
-
  <mi> EtetR</mi>
+
-
</mrow>
+
-
    </mrow>
+
-
    <mrow>
+
-
<mrow>
+
-
  <mi>&delta;</mi>
+
-
  <mi>TetR</mi>
+
-
</mrow>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
</li>
+
-
<li>
+
-
<math >
+
-
<mrow>
+
-
  <mrow>
+
-
  <mo>K'</mo>
+
-
  </mrow>
+
-
  <mo>=</mo>
+
-
  <mfrac>
+
-
    <mrow>
+
-
<mrow>
+
-
  <mi>RlacI *</mi>
+
-
</mrow>
+
-
<mrow>
+
-
  <mi> ElacI</mi>
+
-
</mrow>
+
-
    </mrow>
+
-
    <mrow>
+
-
<mrow>
+
-
  <mi>&delta;</mi>
+
-
  <mi>LacI</mi>
+
-
</mrow>
+
-
    </mrow>
+
-
  </mfrac>
+
-
</mrow>
+
-
</math>
+
-
</li>
+
-
</ul>
+
-
+
-
<p>
+
-
After manipulation with these reduced parameters, we get this following equations:
+
-
</p>
+
-
<img src="https://static.igem.org/mediawiki/2011/b/be/System_diff_2.png" class="centerwide" style="box-shadow: none"/>
+
-
<p>
+
-
From these equations, we get these figures:
+
-
</p>
+
-
<img src="https://static.igem.org/mediawiki/2011/a/ad/Plate_isocline_medium.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 1:
+
-
</strong>
+
-
Nullclines for [aTc] = 1E-6 M and [IPTG] = 1,55 E-4 M.
+
-
</div>
+
-
<p>
+
-
The nullclines are sketched in the figure below. The red line represents the first equation of the system and the green line, the second equation.
+
-
This figure was obtained with [aTc] = 1E-6 M and [IPTG] = 1,55 E-4 M. These parameters reflect the situation
+
-
of our device in the center of the plate to a logarithmic gradient of IPTG of 1E-6 M to 1E-2 M
+
-
</p>
+
-
<p>
+
-
Three stationary points emerge from this graph. These are the three points of intersection of two curves and represent
+
-
the steady state of the system.
+
-
</p>
+
-
<p>
+
-
The curves intersect in three different points, meaning that the system has three steady states.
+
-
One of them is unstable: the middle one. It represents the point where both relative concentrations are equal,
+
-
which almost never happens in the reality, since the two repressors inhibit each other.
+
-
Any fluctuation will lead one repressor to take an advantage on the other.
+
-
</p>
+
-
<table class="nobordure">
+
-
<tr>
+
-
<td><img src="https://static.igem.org/mediawiki/2011/c/cf/Plate_isocline_Left.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 2:</strong>
+
-
Nullclines for the left side of the plate
+
-
</div></td>
+
-
<td><img src="https://static.igem.org/mediawiki/2011/b/b4/Plate_isocline_Right.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 3:</strong>
+
-
Nullclines for the right side of the plate
+
-
</div></td>
+
-
</tr>
+
-
</table>
+
<p>
<p>
-
The left graph represents the left side of the plate: aTc concentration is superior to IPTG concentration
+
To see the results we obtained with this algorithms, refer to this <a href="https://2011.igem.org/Team:Grenoble/Projet/Results">page</a>.
-
and the right graph represents the right side of the plate where IPTG concentration prevails.
+
</p>
-
These figures show that when the concentration of one of the repressors is higher, the system is no longer bistable but monostable.
+
-
</p>
+
-
<p>
+
-
Points to Remember :
+
-
</p>
+
-
<ul>
+
-
<li>
+
-
On the extreme side of the plate, the system is monostable.
+
-
</li>
+
-
<li>
+
-
On the switch area of the plate, the system is bistable.
+
-
</li>
+
-
<li>
+
-
Bistability, in the switch area, allows us to obtain neighboring bacteria in different states.
+
-
These bacteria can communicate together(see the Design and Principle section) and stimulate the coloration.
+
-
</li>
+
-
</ul>
+
-
+
-
<h3>Hysteresis</h3>
+
-
<p>
+
-
The goal of the hysteresis study is to established the switch conditions when the toggle switch is already blocked in a predefined way.
+
-
In our mathematical studies, we blocked the system in the lacI way with different preliminary aTc concentrations.
+
-
To get hysteresis curves, after blocking the system, we grow the amount of IPTG to see from which concentration the system will switch. Then, we decrease
+
-
IPTG concentration to see if the system switch back to the initial state at the same IPTG concentration.
+
-
The blue curve shows the evolution of TetR concentration when IPTG concentration increases.
+
-
The red curve shows the evolution of TetR concentration when IPTG concentration decreases.
+
-
</p>
+
-
<img src="https://static.igem.org/mediawiki/2011/5/55/Hysteresis_10-6.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 4:</strong>
+
-
Hysteresis curve of the system.
+
-
</div>
+
-
<p>
+
-
Important values to exploit from these curves are the two switch concentration of IPTG.
+
-
On this curve, we can get the switch up concentration: ~ 1E-2 M of IPTG and the switch back concentration ~ 3E-5 M.
+
-
</p>
+
-
<p>
+
-
The switch back concentration is very similar to the dissociation constant between lacI and IPTG (which is 2.96E-5 M).
+
-
It means that, when there is not enough IPTG in the bacteria, the IPTG-lacI complexe is faster degraded than produced.
+
-
So the repression is no longer effective.
+
-
</p>
+
-
<p>
+
-
The following curves show different hysteresis for growing aTc concentrations.
+
-
</p>
+
-
<table class="nobordure">
+
-
<tr>
+
-
<img src="https://static.igem.org/mediawiki/2011/6/65/Hysteresis_10-9.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 5:</strong>
+
-
Hysteresis for [aTc] = 1E-9 M
+
-
</div>
+
-
</tr>
+
-
<tr>
+
-
<img src="https://static.igem.org/mediawiki/2011/c/ca/Hysteresis_10-8.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 6:</strong>
+
-
Hysteresis for [aTc] = 1E-8 M
+
-
</div>
+
-
</tr>
+
-
<tr>
+
-
<img src="https://static.igem.org/mediawiki/2011/1/12/Hysteresis_10-7.png" class="centerwide" style="box-shadow: none"/>
+
-
<div class="legend">
+
-
<strong>Figure 7:</strong>
+
-
Hysteresis for [aTc] = 1E-7 M
+
-
</div>
+
-
</tr>
+
-
</table>
+
-
+
-
+
-
<p>
+
-
The two first curves (for aTc = 1E-9 M and aTc = 1E-8 M) show that the switch up and switch back concentrations are the same. This concentration is
+
-
~ 3E-5 M, the dissociation constant between lacI and IPTG.
+
-
The last curve (for aTc = 1E-7 M) shows that the switch back concentration stay the same.
+
-
But the switch up concentration is higher. In fact, for aTc concentration superior to 1E-7 M, the switch up concentration is growing with aTc concentration.
+
-
</p>
+
-
<p>
+
-
The concentration of aTc 1E-7 M appears to be the limit of sensibility to the toggle switch. This concentration represents the dissociation constant of
+
-
aTc to TetR repressor.
+
-
</p>
+
-
<p>
+
-
Points to Remember :
+
-
</p>
+
-
<p>
+
-
From this mathematical study, we can get the limit of detection of our system: which is close to the dissociation constant of aTc and its repressor.
+
-
</p>
+
-
+
</div>
</div>
-
<div id="selector">
+
 
 +
<center>
<form method="get" >
<form method="get" >
-
  <input type="button" value="< PREVIOUS <" onclick="document.location = '/Team:Grenoble/Projet/Modelling#Content';" />
+
  <input type="button" value="< PREVIOUS <" onclick="document.location = '/Team:Grenoble/Projet/Modelling';" />
  <select name="id" onchange="document.location = '/Team:Grenoble/Projet/Modelling' + this.options[this.selectedIndex].value ;">
  <select name="id" onchange="document.location = '/Team:Grenoble/Projet/Modelling' + this.options[this.selectedIndex].value ;">
Line 2,164: Line 400:
    </optgroup>
    </optgroup>
-
    <optgroup label="Deterministic Modelling" >
+
    <optgroup label="Construction of the model" >
                                  
                                  
-
                                     <option value="/Deterministic#Our_EquationsTS" selected="selected">Our equations - Toggle switch</option>
+
                                     <option value="/Deterministic#Our_EquationsTS" selected="selected">Establishment of the equation - Toggle switch</option>
-
                                     <option value="/Deterministic#Our_EquationsQS" >Our equations - Quorum sensing</option>
+
                                     <option value="/Deterministic#Our_EquationsQS" >Establishment of the equation - Quorum sensing</option>
                                  
                                  
                                     <option value="/Deterministic#Our_algorithms" >Our algorithms</option>
                                     <option value="/Deterministic#Our_algorithms" >Our algorithms</option>
-
                               
 
-
                                    <option value="/Deterministic#Isoclines">Isoclines and Hysteresis</option>
 
                                  
                                  
                                      
                                      
Line 2,179: Line 413:
                             <optgroup label="Stochastic Modelling">
                             <optgroup label="Stochastic Modelling">
                                  
                                  
-
                                     <option value="/Stochastic#Geof">Geof's</option>
+
                                     <option value="/Stochastic#Geof">Sensitivity to noise</option>
                                  
                                  
                                     <option value="/Stochastic#Gillespie_algorithm">Gillespie algorithm</option>
                                     <option value="/Stochastic#Gillespie_algorithm">Gillespie algorithm</option>
Line 2,189: Line 423:
                             <optgroup label="Parameters">
                             <optgroup label="Parameters">
                              
                              
-
    <option value="/Parameters">Our parameters</option>
+
    <option value="/Parameters">Table of parameters</option>
-
 
+
-
    </optgroup>
+
-
                           
+
-
                            <optgroup label="Results">
+
-
                           
+
-
    <option value="/Results#Validation">Validation of our Network</option>
+
-
 
+
-
    <option value="/Results#Device">Device specificities</option>
+
    </optgroup>
    </optgroup>
Line 2,206: Line 432:
                  
                  
             </form>
             </form>
 +
            </center>
 +
             </div>
             </div>

Latest revision as of 03:07, 29 October 2011

Grenoble 2011, Mercuro-Coli iGEM


Construction of the model

PDF version of the next two sections (Equations for Toggle Switch and Quorum sensing)

As a proof of concept, we will consider anhydrotetracycline (aTc) instead of Mercury in our model, and the transcriptional regulator TetR in place of MerR. The TetR system is well characterized in E. coli, which facilitates the modelling. In addition, if the system works well with aTc, it should work as well with Mercury, Copper or lead for example.

In addition, since aTc diffuse freely accross the membrane of the cell, we do not have to take complex uptake mechanisms into considerations. Mercury is ionized and its entry in the cells depends on the presence of transporter protein.
So in the following chapter, we are going to use TetR instead of MerR and aTc instead of Mercury.

The Two modules of Modelling

Large-scale biochemical networks are classically decomposed into modules of smaller size to facilitate the model building process and the model calibration. The approach consists in modelling each module separately and integrating the different models into a larger model of the whole system. Like divided our genetic network in severals part (see genetic network), we also divided our model in two independant level of modelling:

  • The Toggle Switch module: modelling this network module allows to predict in which state the bacteria are. In particular, we can determine the switching conditions in bacteria and the localization of the switching area on the device (that depend on both IPTG and aTc concentrations). This gives indications on how to adjust the size of the device to improve the aTc detection.
  • The Quorum Sensing and Coloration module:the corresponding model is used to predict the localization and the width of the red line on the device. The modelling results are used to improve the device precision, for instance, by choosing between a device with a continuous bacterial layer and a device with strips containing bacteria. Each strip has the same concentration of aTc, but a different IPTG concentration.

The first level of the model will allow us to define the switch conditions in bacteria, depending on the concentrations of aTc and IPTG. From these results, we could see where the switch zone will appear on the device and therefore, the position of the red line. These parts of the results indicate the range of aTc that can be detected.

The second level will give us an estimation of the red line width, which indicates the system precision. Based on these results, we could improve the precision of our device, for instance, by comparing between a device with a continuous bacterial layer and a device with strips containing bacteria. Each strip has a different IPTG concentration, but the same concentration of Mercury.

Two independent levels of modelling which are coupled in order to get a global simulation of the device.

Establishment of the equation

Toggle switch

In a first part, we define a model to caracterize the Toggle Switch module of our genetic network.

  1. Biological Model

    2. A toggle switch consists of two genes, each coding for a protein that represses the expression of the other gene. This double repression system ensures the basic function of a toggle switch: a bistable system which can be switched from one state to the other by putting, in our example, some IPTG or aTc molecules in the medium.

    The biological system we are trying to implement is more complex, on both the biological and physical side. However, the toggle switch model is basically the same. In the study of the toggle switch itself, the system can be reduced to a simple two-state subsystem that we will then use for the rest of our modelling. However, our toggle switch model is basically the same: we can reduce it to a simple two-state subsystem that we will then use for the rest of our modelling. The toggle switch itself is not influenced by the rest of the system, if we do not consider the RsmA regulatory system that will be modeled at the very end of our work. Thus we will be able to model the toggle switch independently and then build the rest of the model upon this basis.

  2. Mathematical Model

    3. In order to get the state of the bacteria, we need to compute the concentration of both repressors. To obtain these variations, we develop a system of ordinary differential equations (ODES) which governs the behavior of the Toggle Switch.

    $ \frac{d[TetR]}{dt} = \frac{k_{pLac}.[pLac]_{tot}}{1 + (\frac{[lacI]}{K_{pLac} + \frac{K_{pLac}.[IPTG]}{K_{lacI-IPTG}}.})^\beta} - \delta_{TetR}.[TetR]$

    $\frac{d[lacI]}{dt} = \frac{k_{pTet}.[pTet]_{tot}}{1 + (\frac{[tetR]}{K_{pTet} + \frac{K_{pTet}.[aTc]}{K_{TetR-aTc}}.})^\gamma} - \delta_{lacI}.[lacI]$

    With this ODE system, we follow the evolution of the concentration of the two toggle switch repressors, TetR and LacI. This gives us the state of the bacteria. A demonstration of this ODE system is available in the previous pdf file. We briefly explain the equations below.

    Both equations are developed following the same approach. There is a term of production and a term of degradation. The parameters $k_{pLac}.[pLac]_{tot}$ represent the protein synthesis rate from the pLac promoter. K_{pLac} and K_{lacI−IPTG} are the dissociation constants of LacI and pLac, and LacI and IPTG, respectively. The parameters β and γ denote the cooperativity of repression, that is, the number of repressors bound to the promoter.

    According to these equations, the rate of variation of repressor TetR is inhibited by the repressor LacI. The degree of inhibition is modulated by the IPTG concentration. Reciprocally in the second equation, the rate of variation of LacI depends on TetR, whose negative effect is modulated by aTc.

    This indicates that the two equations are coupled. And also that only one repressor could be predominant, as shown later.

    These two equations can be easily computed with a differential solver. We can precisely estimate the effects of each parameter.

With this model, we were able to predict the behavior of our toggle switch.

Establishment of the equation

Quorum sensing

  1. Mathematical Model

    2. In a second part, we define a model able to characterize the quorum sensing module of our genetic network, which involves the quorum sensing genes CinI and CinR, as well as the signaling molecule AHL.
    In order to model the Quorum Sensing module, we detail below the different reactions taking place inside this module. For reasons that will become clear later, we focus on a particular area of our device, where neighboring bacteria will have a different behavior, although they carry the same genetic circuit.

    Figure 1:Mechanism of Quorum Sensing diffusion at the boundary

    According to the figure, several must be taken into account:

    1. the production of the Quorum Sensing molecule
    2. the secretion of the molecule
    3. the diffusion of the molecule in the medium
    4. the penetration of the molecule
    5. the complexation of the molecule with its receptor
    6. the activation of the coloration

    To model these mecanisms, we need to follow the evolution of the following quantities

    • $[QS_i]$ concentration of the intracellular Quorum Sensing molecule.
    • $[QS_e]$ concentration of the extracellular Quorum Sensing molecule.
    • $[cinR]$ concentration of the Quorum Sensing receptor.
    • $[cinI]$ concentration of the Quorum Sensing producer enzyme.
    • $[cinR_{comp}]$ concentration of the complexe cinR-QS.

    Based on the Bangalore 2007 iGEM team, we get the following system of equations:

    $\frac{d[QS_i]}{dt} = \eta([QS_e]-[QS_i])-\delta_{QSi} [QS_i] + k_{QS-production}'[cinI]$

    $\frac{d[QS_e]}{dt} = \rho v_c\eta([QS_i]-[QS_e])-\delta_{QSe} [QS_e] + D_{diff}\frac{\partial^2 [QS_e]}{\partial x^2}$

    $\frac{d[cinR_{free}]}{dt} = \frac{k_{pLac}.[pLac]_{tot}}{1 + (\frac{[lacI_{total}]}{K_{pLac} + \frac{K_{pLac}.[IPTG]}{K_{lacI-IPTG}}.})^\beta} - \delta_{cinR}[cinR_{free}] - V_{complexation}$

    $\frac{d[cinR_{comp}]}{dt} = K_{comp}([cinR_{free}].[QS_i])$

    In the first equation, expressing the evolution of the concentration of the intracellular Quorum Sensing molecule, 3 terms are involved: $[QSe]−[QSi]$, which describes the diffusion through the membrane, $\delta_{QSi}[QSi]$, the degradation and $k_{QS−production}[cinI]$, the production of Quorum Sensing molecule by the enzyme CinI. In the second equation, expressing the evolution of extracellular Quorum Sensing, there is no production term, but a spatial diffusion term $D_{diff}\frac{\partial^2 [QS_e]}{\partial x^2}$.

    The concentrations of CinI and CinR can be obtained by using the toggle switch modelling. Indeed, since CinI is on the pathway of LacI and CinR on the pathway of Tet, their evolution follow the same equations. In addition we consider the complexation of the CinR protein and the Quorum Sensing molecule, which is expressed by the term $V_{complexation}$ in the CinR equation: \[V_{complexation} = K_{comp}[QS_i][CinR_{free}]\] with $K_{comp}$ the affinity constant of AHL for cinR.

    In order to simplify the model, we considered that the complexation of CinR to AHL is total and depends only on $[cinR]$ and $[QS_i] which is the limitant factor$.

    To solve this set of equations, we couldn't use a classical ODE solver from Matlab (Mathworks), because the equations are derived both in time and space. We therefore needed to use the finite difference method. To that aim, we build a matrix based on Taylor's series discretization.

  2. Definition of the matrix

    3. To solve this set of equations we have to use a matrix that will describe our system in both space and time. for example for the QS molecule outside of the cell :

    $M_{QSe}(m,n) = [QS_e](x,t)$
    $M_{QSe}(m+1,n+1) = [QS_e](x + dx,t+dt)$

    In these equations, m represents the spatial dimension and n the temporal dimension.

    • On the spatial point of view, we only consider the x dimension, as the IPTG gradient will be only evolving along this dimension. Thus we consider the state of our cells is the same along the width of our plate.
    • With this Matrix, and after computation of all the terms, we can get the entire behaviour of CinI, CinR, QS inside and outside the cells.
    • The first line of the Matrix equals 0. These are the initial conditions we set to 0 at time t = 0s.
    • On the borders of the plate (x = 0 and x = L) the model used has to be different, limit conditions will be set.
    • Of course, QSi, CinI and CinR matrices will be similarly implemented.
  3. Discretization of the equation

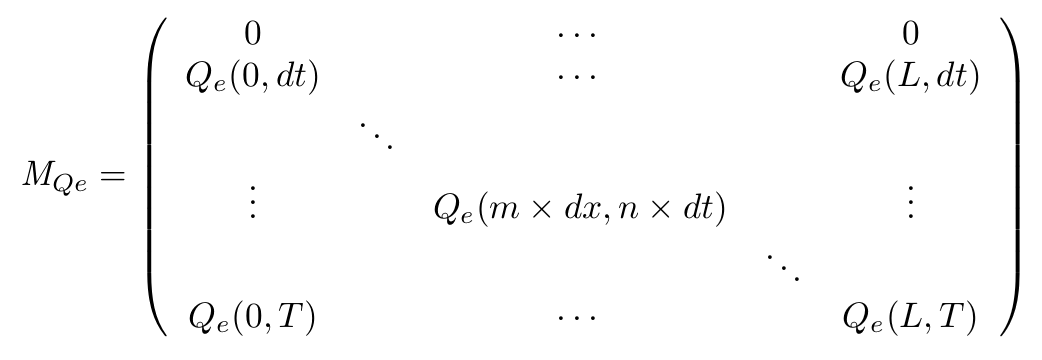
    4. With our continuous equations set, we want to obtain discrete definition of each of the matrices. interdependencies of the equations imply that the computation of the matrices will be performed on the entire CinI matrix first, then each line of the Qi and Qe matrices will be computed alternatively. The computation of the CinR will be eventually performed.

    Parallel computation of all the matrices without proper control is not possible indeed, as the terms of Qi matrix will depend on the Qe terms of the preceding line (and vice-versa). Discretization is obtained with first order taylor series :

$ M_{QSi}(m,n+1) =\Delta t (\eta (M_{QSe}(m,n) - M_{QSi}(m,n)) - \delta_{QSi}.M_{QSi}(m,n) + k_{QSp}M_{CinI}(m,n)) + M_{QSi}(m,n) $

$ M_{QSe}(m,n+1) =\Delta t ( D_{m} + D_{diff} \frac{M_{QSe}(m+1,n) - 2 M_{QSe}(m,n) + M_{QSe}(m-1,n)}{\Delta x^2}) + M_{QSe}(m,n) $

$ with D_{m} =\rho v_c \eta .M_{QSi}(m,n) - M_{QSe}(m,n)(\delta_{QSe} + \rho v_c \eta) $

$ M_{CinR_{free}}(m,n+1) = \Delta t (\frac{k_{pTet}[P_{Tet total}]}{1+ (\frac{[TetR]}{K_{pTet}(1+\frac{[aTc]}{K_{TetR - aTc}})})^{n_{pTet}}} - M_{CinR_{free}}(m,n)(\delta_{CinR} - k_{comp}.M_{Qi}(m,n))) + M_{CinR_{free}}(m,n)$

With these discrete equations the 4 matrices can be computed through simple calculation loops over each line. The CinI matrix does not depend on space dimension, it is then possible to compute it without discretization with a differential solver.

Moreover to get the coupling of toggle switch and quorum sensing modules, we used the results of the first one (lacI and TetR evolution) to get the evolution of quorum sensing proteins (respectively cinI and cinR). It means that the output of the first module are used as input for the second module.

With this model, we were able to predict how the red stripe appears on the plate

Our algorithms

An archive containing our Matlab scripts for the deterministic modeling can be found here (file Deterministic_archive.tar.gz). You can launch and ODE-based simulation(see our ODEs in the two previous sections) with the file biosenseur1Dmain.m.

Several dialog boxes will pop up to enter the specificities of the simulation: (physical specificities of the device, chemical species concentrations and IPTG gradient).

At the end of the simulation you obtain 3 matrices named M_stock, M_QS and M_comp containing the concentrations in each protein species at each time point and on each physical point of the plate. We wrote three Matlab scripts (DynamicplottingTS, DynamicplottingQS and DynamicplottingCP) that dynamically display the protein concentrations. For a good understanding of the models and of our results, we also wrote a script (Imageshow.m) to illustrate the plate coloration.

To see the results we obtained with this algorithms, refer to this page.

Retrieved from "http://2011.igem.org/Team:Grenoble/Projet/Modelling/Deterministic"