Team:Peking S/project/nonb

From 2011.igem.org

(Difference between revisions)
 
(26 intermediate revisions not shown)
Line 7: Line 7:
-
<font color="#ffffff"> <font size=6>Non-Boolean Dynamics</font></font>
+
 
-
<br>
+
<font color="#ffffff"> <font size=6>Non-Boolean Population</font></font>
 +
<br><br>
{{Template:Http://2011.igem.org/Team:Peking S/nonboolean}}
{{Template:Http://2011.igem.org/Team:Peking S/nonboolean}}
<br><br>
<br><br>
-
===Introduction===
 
-
Synthesizing a Modular Comparator Using Small Regulatory RNAs
+
By compartmentalizing molecular components of a complex genetic circuit or a pathway, engineered microbial consortia may perform functions that are difficult for monocultures via '''differentiation''' and '''communication'''. Also, due to metabolic differentiation and possibly an appropriate community structure (e.g., communities without strict competitive hierarchies), microbial consortia may show better endurance in changeable environment.
-
Introduction
+
Recent efforts to engineer microbial consortia primarily focused on either multi-step function performing or population interaction centered dynamics. Apart from several leading attempts in building basic Boolean elements, non-Boolean population dynamics appear to be versatile in both trends. Bidirectional communication-based population interactions (e.g. the synthetic prey-predator ecosystem) have been achieved, but a tri-population circuit with double-bidirectional communication would be an adventurous attempt. It is also an appropriate demonstration for our ‘chemical wire’ toolbox.
-
Our ‘chemical wire’ toolbox is not only applicable to Boolean logic gene networks, but also amenable to non-Boolean population dynamics, for instance, the microbial population density balancer mentioned above.  
+
Inspired by the fact that integration and comparison of signals is less frequently involved in the construction of intercellular genetic networks, we also hope to fill this blank with our small-RNA based comparator in the monitoring cells.  
 +
-
In such a dynamical network, we need to construct a comparator device that can integrate two environmental signals. We managed to fulfill the task with the simplest elements and types of interactions of gene regulation, i.e., the inducible promoters, mRNAs and regulatory small RNAs that silence them. We will demonstrate that simply by combining these three types of genetic components, a comparator module can be implemented and thus to work in population balancer system to verify the feasibility of our "chemical wire" toolkit for non-Boolean population dynamic.
+
<center>[[File:ABC_system_illustration.png|600px]]</center>
-
Design
 
-
Small noncoding RNAs (sRNAs) have been depicted in recent years to play central roles in gene regulation. The special features of small RNA mediated regulation are fast responsive, noise insensitive and threshold effect, which inspire us to construct an artificial comparator based on small RNA regulation. Before biological implementation in bench, during circuit design, series of requirements must be met.
+
<center>''Figure 1. Schematic of our population density balancer.''</center>
-
(1) Input 1 activates mRNA and sRNA 1.
 
-
(2) Input 2 activates mRNA and sRNA 2.  
+
Aiming at a hierarchal regulation of population growth, signaling molecules report cell densities of the two competing populations and the corresponding feedback signals are essential. Here we harnessed two quorum sensing modules, RhlI/RhlR from ''Pseudomonas aeruginosa'' and CinI/CinR from ''Rhizobium leguminosarum'' to enable two-way communications between A cells and C cells. Meanwhile the rewired salicylate regulated PchBA/NahR module and the LasI/LasR quorum sensing devices from Pseudomonas aeruginosa are utilized for B-C bidirectional communication. CinI/CinR & PchBA/NahR systems are carefully characterized in our ‘chemical wire’ toolbox module and all four signaling systems are validated for their orthogonality. [https://2011.igem.org/Team:Peking_S/project/wire    Check ]our ‘chemical wire’ toolbox page for more information.  
-
(3) Suppose there is more input 1, sRNA 1 will strongly repress mRNA 2 and vice versa.
 
-
(4) Suppose there is less input 2, the repression going towards the other way should be weak enough. This will lead to the production of output 1, and little to no production of output 2.  
+
<center>[[File:Competitor illustration.png|600px]]</center>
-
(5) The output of the device is either dominated by output 1 or output 2. By seeing which is the case, we can infer whether input 1 or input 2 was present in greater amounts.
 
-
(See Fig. 1)
 
-
[[File:PS_Design.png‎]]
+
<center>''Figure 2. Expected Function of the comparator, C cells ''</center>
-
    ''Fig.1 The design of the sRNA-dependent comparator, as described above''
 
-
Numerous sRNA/5’UTR pair have been reported in literature. We regarded the ptsG/SgrS pair as an ideal candidate for our comparator design for its special regulation mechanism described below.
+
For the sake of effective signal integration, we designed a small RNA based comparator, which is composed of two engineered orthogonal small RNA-mRNA 5’ untranslated region(UTR) pairs. With small RNA from one pair and the target mRNA from the other pair under the control of same inducible promoters, the two pair of RNA regulators interact with each other antagonistically. Under the conditions of A cells dominating, excess C4HSL molecules synthesized by RhlI would lead to a relative overexpression of sgrS2 small RNA regulators, resulting in the silence of ptsG2-cinI mRNA and the consequent lower concentration of 3OH,C14:1-HSL. At the meantime, the expression of sgrS1 and ptsg1-pchBA remain the same and the overall result is a higher output concentration of salicylate. This seems to be a by-pass signaling molecule transition, yet the comparison of relative signal intensity is hard to achieve otherwise`.
   
   
-
Mechanism
 
-
SgrS is an Hfq-binding small antisense RNA that is induced upon phosphosugar stress (Vanderpool, 2007). It forms a ribonucleoprotein complex with RNase E through Hfq to mediate silencing of the target ptsG mRNA encoding the major glucose transporter (Geissmann and Touati, 2004). A 31-nt-long stretch in the 3’ region of SgrS is partially complementary to the translation initiation region of ptsG mRNA, and a 6 nt region overlapping the Shine-Dalgarno sequence of the target mRNA turns out to be crucial for SgrS’ function, shown as Fig 2 (Kawamoto et al., 2006; Maki et al., 2010).
+
<center>[[File:CELLS A&B.png|600px]]</center>
-
[[File:M_Mechanism.png‎]]
 
-
[[File:M_P1_S1.png‎]]
+
<center>''Figure 3. Components of A&B Cells''</center>
-
[[File:M_P2_S2.png‎]]
 
-
''Fig. 2 Sequence alignment of wild type ptsG/SgrS pair and its mutant complementary pairs.
+
A cells and B cells basically consist of two discrete modules: a reporting module and an inducible suicide device. The reporting module constitutively express distinct signaling molecules as well as fluorescent proteins and consequently the total concentration of the molecule in culture broth together with the fluorescence strength will clearly indicate the corresponding population density. Inducible promoters in this module are specifically designed for adjusting. The suicide module is directly regulated by chemical signals from C cells, as Figure 3 illustrates.
-
(A) The partial complementary region of ptsG (wt) mRNA and its corresponding sRNA SgrS.(B) The complementary pair of ptsG1 mRNA and corresponding SgrS1.(C) Another complementary pair site-mutant version of ptsG2 mRNA and corresponding SgrS2.''
+
-
Teppei Morita et.al’ s work suggests that two mutations (C85G and C87G) in ptsG mRNA could completely impair the ability of SgrS to downregulate its expression, while compensatory mutations of SgrS (G178C and G176C) restore the gene silencing ability. These results indicate that it is the base pairing of the two RNAs rather than particular nucleotides that is important for SgrS action. They have also illustrated that sequence outside this region, even though complementary, is rather dispensable for the efficient silencing (Kawamoto et al., 2006). This makes mutant ptsG/SgrS pairs orthogonal to genetic context of the host cell.
+
To make our balancer tunable, we introduced a tandem riboswitch responding to different thiamine pyrophosphate (TPP) concentrations. A sufficient TPP concentration results in transcription pre-termination, and thus downstream gene expression is inhibited to some extent. The transcription regulator is placed right after the rhl activated promoters in our system, as shown in Figure 2.
 +
-
By employing two sets of mutant ptsG mRNA as well as its complementary SgrS in the design shown in Fig 1, we set to biologically implement the comparator. In detail, ptsG1 refers to a C85G mutant of ptsG (wt) while ptsG2 is a C87G mutant. SgrS1 (G178C) and SgrS2 (G176C) are the corresponding revertants which could help restore their complementarity. And as a proof-of-concept experiment, we constructed synthetic gene circuits, in which the 5’ untranslated region of ptsG mRNA was translationally fused to the coding sequence of the reporter gfp (Levine et al., 2007), as shown in Fig 3.
+
[[File:TPP.png|680px]]
-
[[File:M_Induce_ptsG.png‎]]
 
-
[[File:M_Induce_SgrS.png‎]]
+
''Figure 4. Sequence and the secondary structure of the tandem TPP riboswitch (Rüdiger Welz and Ronald R. Breaker,2007). The riboswitch carry mutations in the junction in the first aptamer(G41C, A42U) disrupting TPP binding.''
-
''Fig. 3 The modular components of the comparator.'' ''(A) Salicylate leads to the transcription of ptsG-gfp mRNA, which is the target of constitutively expressed SgrS. This is how we implemented both reporting and repressing outputs as a result of the activation of Psal. When there is more salicylate in the media, the GFP fluorescence intensity is expected to be stronger. (B) Salicylate leads to the transcription of SgrS, while the ptsG-gfp mRNA is downstream a constitutive promoter. In this scenario, as the concentration of salicylate increases, the repression effect SgrS exerts on ptsG would in turn be stronger, so the GFP fluorescence intensity is supposed to be weaker.''
 
-
Data Analysis and Discussion
+
An ordinary differential equation (ODE) model was built to simulate population behaviors of our system. The results predicted that our population dynamic balancer can control A(B) cell with arbitrary proportion and the whole system always gets to a steady state without oscillation. [https://2011.igem.org/Team:Peking_S/modeling/summary    Click] to check our model page for more information.
-
 
+
-
To qualitatively and quantitatively characterize the performance of our competitor, we conducted the following experiments.
+
-
 
+
-
Part I. The Orthogonal Silencing Matrix
+
-
 
+
-
The repression capacity of each ptsG/SgrS pair was indicated by the ratio of the average fluorescence intensity before to after the trigger of SgrS. What we expected was a significant repression within the cognate pairs (ptsG1/SgrS1, ptsG2/SgrS2, and ptsG (wt)/SgrS (wt)), and a minor repression folds among different pairs.
+
-
 
+
-
As Figure 4 shows, the highest ratio lie at the diagonal from the upper left to the lower right as expected, which is 5 to 6 folds. As for the ptsG (wt)/SgrS1&2, ptsG1/SgrS (wt), and ptsG2/SgrS (wt), given that these crosses differ at only one base pair, the repression efficacy is around 3 folds. By contrast, the inhibiting effect of on ptsG2 and SgrS2 on ptsG1 is rather unapparent, which can be seen as an appropriate characteristic fitting our competitor requirements.
+
-
 
+
-
The original data also provided below (Table 1).
+
-
 
+
-
[[File:M_Matrix.png‎]]
+
-
 
+
-
''Fig. 4 A graphical representation of the repression matrix associated with SgrS and its mutants, and ptsG and its mutants. The values represent the repression ratios, defined as the repression capacity of each ptsG/SgrS pair, denoted by the ratio of fluorescence intensity before to after the induction of SgrS, suggesting within-subgroup pairwise specificity.''
+
-
 
+
-
''Table 1 Original Data for the ptsG/SgrS Interaction Matrix''
+
-
 
+
-
[[File:M Original Data.png]]
+
-
 
+
-
Part II. Response Curves
+
-
 
+
-
The sRNA-mediated gene silencing can be formulated quantitatively via a simple kinetic model. The model is cast in terms of two mass-action equations for the cellular concentrations of the sRNA (s) and its target mRNA (m):
+
-
 
+
-
[[File:M_model.png‎]]
+
-
 
+
-
The parameters are defined as in Table 2.
+
-
 
+
-
''Table 2. Model Parameters: Definitions and Estimated Values''
+
-
 
+
-
[[File:M_Parameters.png‎]]
+
-
 
+
-
Levine et. al’s work has revealed that in the idealized scenario when binding between sRNA and mRNA occurs extremely rapidly, gene expression is completely silenced if the target transcription rate is below a threshold. Above this threshold, gene expression will increase linearly. Such threshold-linear model is based on the difference of transcription rates between sRNA and mRNA(Levine et al., 2007).
+
-
 
+
-
[[File:M Model 1.png]]
+
-
 
+
-
[[File:M Model 2.png]]
+
-
 
+
-
''Fig 5. Threshold-Linear Response of the Target Gene (in our case, ptsG-GFP mRNA or SgrS). Predicted response curve of a target gene. (a) The red line depicts the idealized threshold-linear mode of regulation in which gene expression is completely silenced if the SgrS transcription rate exceeds a threshold set by the transcription rate of the ptsG-gfp mRNA. Under this threshold, gene expression decreases linearly with the difference between the mRNA and sRNA transcription rates. (b) The red line depicts the idealized threshold-linear mode of regulation in which gene expression is completely silenced if the ptsG-gfp mRNA transcription rate is below a threshold set by the transcription rate of the sRNA. Above this threshold, gene expression increases linearly with the difference between the mRNA and sRNA transcription rates. The idealized scenario is expected when binding between sRNA and mRNA occurs extremely rapidly. The blue line is the actual response expected using the estimated parameters of Table 2.''
+
-
 
+
-
To verify this, we performed experiments to get the dose-response curve. The result is shown in Figure 6.
+
-
 
+
-
[[File:M Integrated 3.png]]
+
-
 
+
-
[[File:M Pw Sw induce ptsG.png]]
+
-
 
+
-
''Fig. 6 The dose-response curve of SgrS/ptsG-gfp interaction. (A) Salicylate-induced SgrS repressing the expression of ptsG-GFP. The promoter activity is defined as the GFP expression of the Psal+gfp strain grown in identical media. Different promoter activities were obtained by varying salicylate concentration in the media. The conjugate pairs fit into dose-response curve with variable Hill slope given as a parameter, and the R^2 is 0.9974, 0.9879, and 0.9607 corresponding to ptsG(wt)/SgrS(wt), ptsG1/SgrS1 and ptsG2/SgrS2, respectively. (B) When sgrS (wt) was constitutively expressed and ptsG (wt) salicylate-induced, a dose-response curve is also fitted with an R^2 of 0.9301.''
+
-
 
+
-
Such results are in accordance with Levine et. al’s conclusion, i.e., the binding rates between mRNA and sRNA in effect are inherently limited, so the threshold-linear model couldn’t be strictly fitted (Levine et al., 2007). But the performance of SgrS/ptsG pairs is very close to the idealized threshold-linear mode of regulation.  
+
-
 
+
-
Methods
+
-
 
+
-
I. The Orthogonal Silencing Matrix
+
-
 
+
-
Materials:
+
-
 
+
-
We have constructed two types of plasmids presented in Figure 7.
+
-
 
+
-
[[File:Plasmid Pc+ptsG+gfp+terminator.png]][[File:Plasmid PBAD+SgrS+terminator.png]]
+
-
''Fig. 7 Plasmids constructed for characterizing ptsG/SgrS orthogonal silencing matrix''
+
[[File:Proportion.png|680px]]
-
After co-transformation to the DH5α competent cells, we got 3×3 strains shown in Table 3.
 
-
''Table 3. E. coli strains constructed for ptsG/SgrS orthogonal silencing matrix.''
+
''Figure 5 Normalized dose-response curve from the ODE simulation. Ka1 stands for transcription rate of ptsG1 and Salicylate Generator. (in bench work, addition of thiamine pyrophosphate, TPP, can modulate this parameter) As Ka1 vary from 1-20 nmol•min^-1,the ratio of A & B cell populations may be arbitrarily modulated from 0.2 to 1''
-
[[File:M Table 3.png]]
 
-
Procedure:
+
In terms of engineering communication with dedicated molecules, population behavior is much density-dependent unless the system spontaneously reaches homeostasis and the ability to maintain consortia with unsteady structure is challenged. Taken all these considerations, we designed a general microfluidic platform for cell-cell communication in chemostat. Our A&B cell co-culture showed tunable population ratio dynamics in our microfluidic device. [https://2011.igem.org/Team:Peking_S/project/microfluidic    Check] the Microfluidic device page for more information.
-
1. Pick a colony to 2ml of LB antibiotic medium, in which the concentration of arabinose is 10-2 mol/L, and every 5 experimental groups are coupled with 2 controls.
 
-
2. Place the induction system at 37 degree for 8 hours.
+
[[File:PkusmfNo6.png|680px]]
-
3. Pellet bacterial cells by 10 min centrifugation at 4200 rpm, discard the supernatant.
 
-
4. Resuspend the pelleted cells in 1000μl of Phosphate Buffered Solution (PBS).
+
''Figure 6. Figure (a) to Figure (h) show the growth of the mixed culture (A cells together with lasI-deficient B cells, referred to as ΔB cells) with inducer generated by CinI (with the initial concentration) inoculated in the upper layer (with the amplification factor of 20, the size of chambers 120μm×120μm, and the intruding velocity of 10μL/h). Photos were taken every one hour, and the time interval lasted three hours. A cells, which were indicated by GFP they expressed, did not grow during this time interval, while B. cells grew vigorously till they filled up the chamber. Figure (a) to Figure (h) illustrate the fact that the inducer generated by CinI could only repress the growth of A cells. Figure (i) and Figure (j) demonstrate the final state of this mixed culture’s growth with salicylate (with the concentration of 10^(-3) mol/L )inoculated in the upper layer, which acted as the inducer designed for inducing the expression of CcdB in ΔB cells( also with the amplification factor of 20, the size of chambers 120μm×120μm, and the intruding velocity of 10μL/h). cells. In this case, A cells finally filled up the chamber, while B. cells kept small population number after three hours’ cultivation.
 +
''
-
6. Transfer 500μl of bacterial resuspension into tubes to test the expression of GFP by flow cytometry.
 
-
II. The Response Curve
+
[[File:PkusmfNo7.png|680px]]
-
We have constructed two types of plasmids shown as Figure 8.
 
-
[[File:Plasmid Pc+ptsG+gfp+terminator.png]][[File:M Plasmid Psal+SgrS+terminator.png]]
+
''Figure 7. Figure (a_1) and (a_2) show the initial state of the mixed culture in the chamber, the number of A cells and that of ΔB cells were almost the same. Then we inoculated the mixture of salicylate with the concentration of 10^(-3) mol/L and the solution which was diluted in fold of 10^5 from the initial solution of inducer generated by CinI, the inducers for A cells and ΔB cells. Figure (b_1), (b_2), (c_1), (c_2), (d_1) and (d_2) show that the ratio of population number of A cells to that of B. cells had changed from the initial state and stayed the same during the two hours, which means that the culture came to a steady state under the control of inducers. Figure (e_1), (e_2), (f_1), (f_2), (g_1), (g_2), (h_1) and (h_2) illustrate the growth of the mixed culture with the mixture of salicylate with the concentration of 10^(-4) mol/L and the solution which was diluted with nutrient solution in fold of 10^4 from the initial solution of inducer generated by CinI. During this time interval, ΔB cells grew fast while A cells were extruded from chamber. In Figure (g_1) and (g_2), the number of ΔB cells decreased a little, mainly because the time-delayed effect of the control of salicylate, but the population soon recovered from the effect. Finally, in Figure (h_1) and (h_2), ΔB cells nearly filled up the whole chamber while there were few A cells in the same chamber.''
-
[[File:M Plasmid Pc+SgrS+terminator.png]][[File:M Plasmid Psal+ptsG+gfp+terminator.png]]
+
-
''Fig. 8 (A) Plasmids constructed for plotting salicylic acid dose-response curve for SgrS. (B) Plasmids constructed for plotting salicylic acid dose-response curve for ptsG''
 
-
Procedure:
+
To sum up, we featured our system with such specifications:
-
1. Pick a colony to 400 milliliter of LB antibiotic medium, in which the concentration of salicylate is set from 10^-8 to 10^-4. Every 6 experimental groups are coupled with 2 controls.
+
'''Multiple ‘chemical wires’ utilization'''
-
2. Place the induction system at 37 degree for 8 hours.
+
'''Multi-population interactions and signal integration'''
-
3. Pellet bacterial cells by 10 min centrifugation at 4200 rpm, discard the supernatant.
+
'''Tunable population behavior'''
-
4. Resuspend the pelleted cells in 1000μl of Phosphate Buffered Solution (PBS).
+
'''Theoretical and physical device supporting'''
-
6. Transfer 100μl of bacterial resuspension into each well of 96-well plate to undergo the enzyme-labeled assay.
+
==References==
-
Reference
+
1．Brenner, K., You, L. C. & Arnold, F. H. Engineering microbial consortia: a new frontier in synthetic biology. ''Trends Biotechnol'' '''26''', 483-489 (2008)
-
1.Geissmann, T.A., and Touati, D. (2004). Hfq, a new chaperoning role: binding to messenger RNA determines access for small RNA regulator. The EMBO journal 23, 396-405.
+
2．Brenner K, Karig DK, Weiss R, Arnold FH (2007) Engineering bidirectional communication mediates a consensus in a microbial biofilm consortium. ''Proc Natl Acad Sci USA'' '''104''': 17300–17304
-
2.Gottesman, S. (2002). Stealth regulation: biological circuits with small RNA switches. Genes & development 16, 2829-2842.
+
3．You, L., Cox, R. S. 3rd, Weiss, R. & Arnold, F. H. Programmed population control by cell–cell communication and regulated killing. ''Nature'' '''428''', 868–871 (2004).
-
3.Kawamoto, H., Koide, Y., Morita, T., and Aiba, H. (2006). Base-pairing requirement for RNA silencing by a bacterial small RNA and acceleration of duplex formation by Hfq. Molecular microbiology 61, 1013-1022.
+
4. Basu S, Gerchman Y, Collins CH, Arnold FH, Weiss R (2005) A synthetic multicellular system for programmed pattern formation. ''Nature'' '''434''': 1130–1134
-
4.Levine, E., Zhang, Z., Kuhlman, T., and Hwa, T. (2007). Quantitative characteristics of gene regulation by small RNA. PLoS biology 5, e229.
+
5. Kerr, B., Riley, M., Feldman, M. & Bohannan, B. Local dispersal and interaction promote coexistence in a real life game of rock–paper–scissors. ''Nature'' '''418''', 171–174 (2002).  
-
5.Maki, K., Morita, T., Otaka, H., and Aiba, H. (2010). A minimal base-pairing region of a bacterial small RNA SgrS required for translational repression of ptsG mRNA. Molecular microbiology 76, 782-792.
+
<html>
 +
<a href="#top">Top↑
 +
</div>
-
6.Vanderpool, C.K. (2007). Physiological consequences of small RNA-mediated regulation of glucose-phosphate stress. Current opinion in microbiology 10, 146-151.
+
</html>

Latest revision as of 03:19, 6 October 2011

Template:Https://2011.igem.org/Team:Peking S/bannerhidden Template:Https://2011.igem.org/Team:Peking S/back2

Template:Https://2011.igem.org/Team:Peking S/bannerhidden

css r corner



Non-Boolean Population

Introduction|Design|Comparator


By compartmentalizing molecular components of a complex genetic circuit or a pathway, engineered microbial consortia may perform functions that are difficult for monocultures via differentiation and communication. Also, due to metabolic differentiation and possibly an appropriate community structure (e.g., communities without strict competitive hierarchies), microbial consortia may show better endurance in changeable environment.

Recent efforts to engineer microbial consortia primarily focused on either multi-step function performing or population interaction centered dynamics. Apart from several leading attempts in building basic Boolean elements, non-Boolean population dynamics appear to be versatile in both trends. Bidirectional communication-based population interactions (e.g. the synthetic prey-predator ecosystem) have been achieved, but a tri-population circuit with double-bidirectional communication would be an adventurous attempt. It is also an appropriate demonstration for our ‘chemical wire’ toolbox.

Inspired by the fact that integration and comparison of signals is less frequently involved in the construction of intercellular genetic networks, we also hope to fill this blank with our small-RNA based comparator in the monitoring cells.


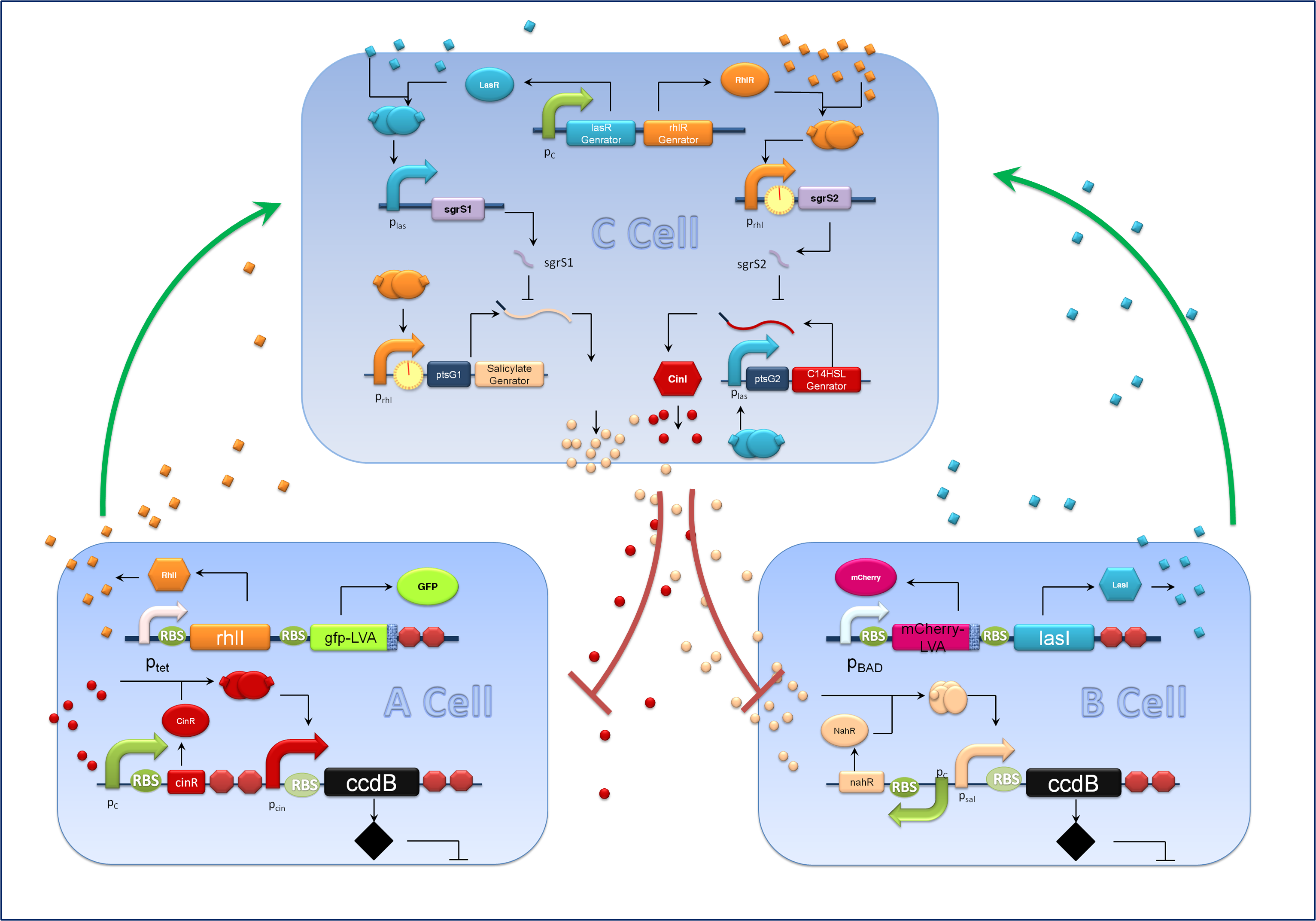
ABC system illustration.png


Figure 1. Schematic of our population density balancer.


Aiming at a hierarchal regulation of population growth, signaling molecules report cell densities of the two competing populations and the corresponding feedback signals are essential. Here we harnessed two quorum sensing modules, RhlI/RhlR from Pseudomonas aeruginosa and CinI/CinR from Rhizobium leguminosarum to enable two-way communications between A cells and C cells. Meanwhile the rewired salicylate regulated PchBA/NahR module and the LasI/LasR quorum sensing devices from Pseudomonas aeruginosa are utilized for B-C bidirectional communication. CinI/CinR & PchBA/NahR systems are carefully characterized in our ‘chemical wire’ toolbox module and all four signaling systems are validated for their orthogonality. Check our ‘chemical wire’ toolbox page for more information.


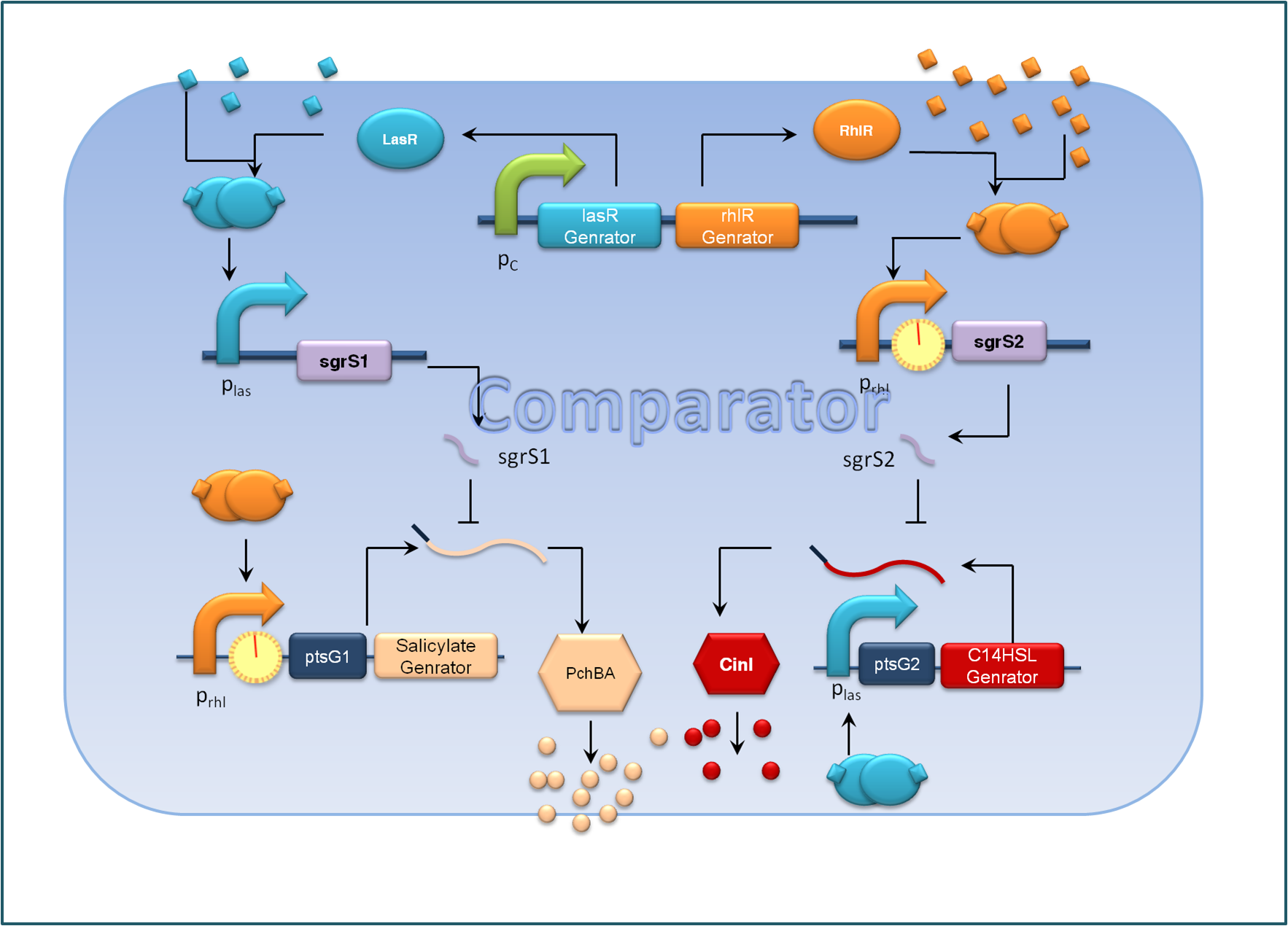
Competitor illustration.png


Figure 2. Expected Function of the comparator, C cells


For the sake of effective signal integration, we designed a small RNA based comparator, which is composed of two engineered orthogonal small RNA-mRNA 5’ untranslated region(UTR) pairs. With small RNA from one pair and the target mRNA from the other pair under the control of same inducible promoters, the two pair of RNA regulators interact with each other antagonistically. Under the conditions of A cells dominating, excess C4HSL molecules synthesized by RhlI would lead to a relative overexpression of sgrS2 small RNA regulators, resulting in the silence of ptsG2-cinI mRNA and the consequent lower concentration of 3OH,C14:1-HSL. At the meantime, the expression of sgrS1 and ptsg1-pchBA remain the same and the overall result is a higher output concentration of salicylate. This seems to be a by-pass signaling molecule transition, yet the comparison of relative signal intensity is hard to achieve otherwise`.


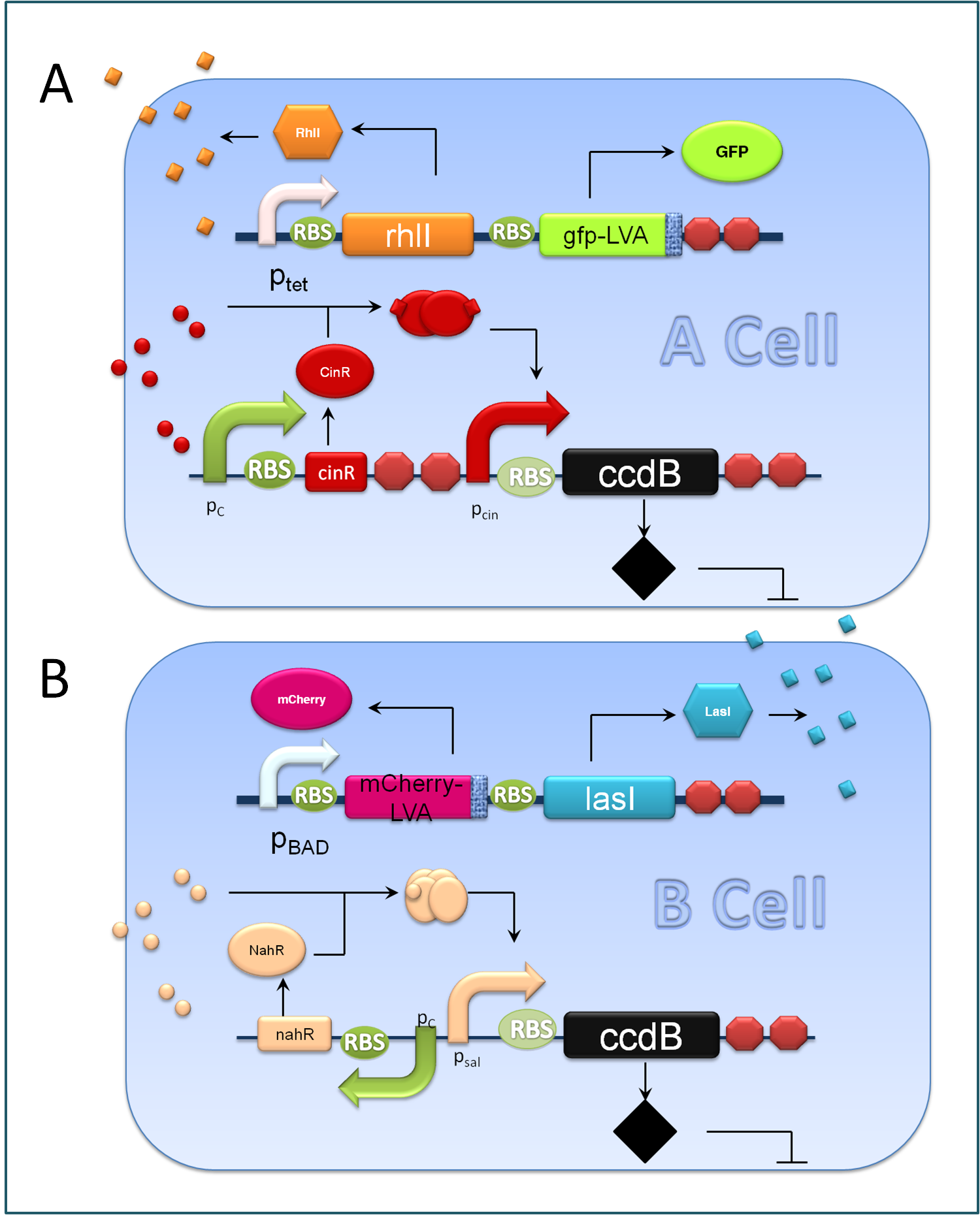
CELLS A&B.png


Figure 3. Components of A&B Cells


A cells and B cells basically consist of two discrete modules: a reporting module and an inducible suicide device. The reporting module constitutively express distinct signaling molecules as well as fluorescent proteins and consequently the total concentration of the molecule in culture broth together with the fluorescence strength will clearly indicate the corresponding population density. Inducible promoters in this module are specifically designed for adjusting. The suicide module is directly regulated by chemical signals from C cells, as Figure 3 illustrates.

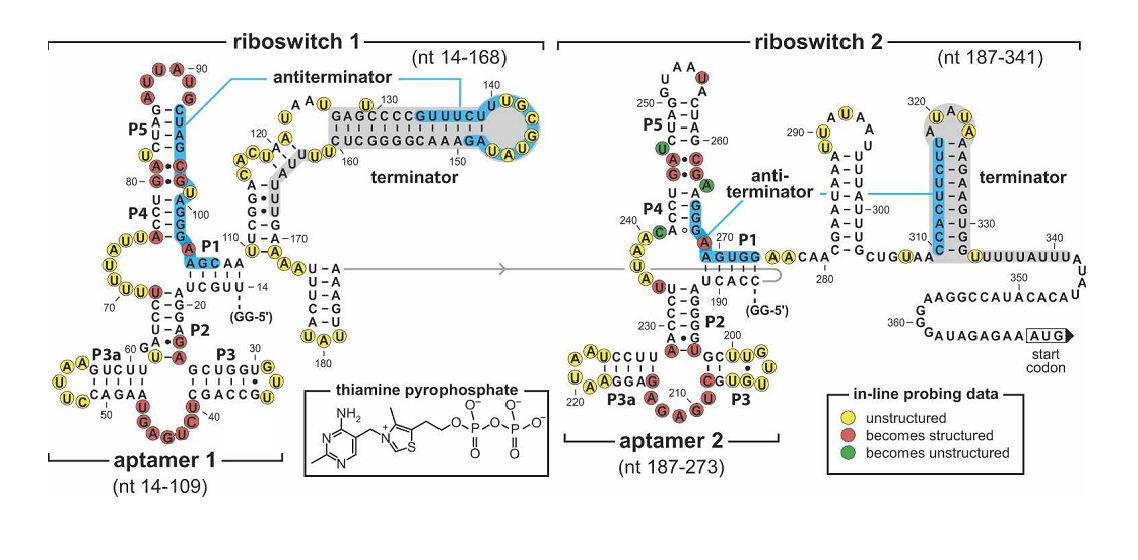
To make our balancer tunable, we introduced a tandem riboswitch responding to different thiamine pyrophosphate (TPP) concentrations. A sufficient TPP concentration results in transcription pre-termination, and thus downstream gene expression is inhibited to some extent. The transcription regulator is placed right after the rhl activated promoters in our system, as shown in Figure 2.


TPP.png


Figure 4. Sequence and the secondary structure of the tandem TPP riboswitch (Rüdiger Welz and Ronald R. Breaker,2007). The riboswitch carry mutations in the junction in the first aptamer(G41C, A42U) disrupting TPP binding.


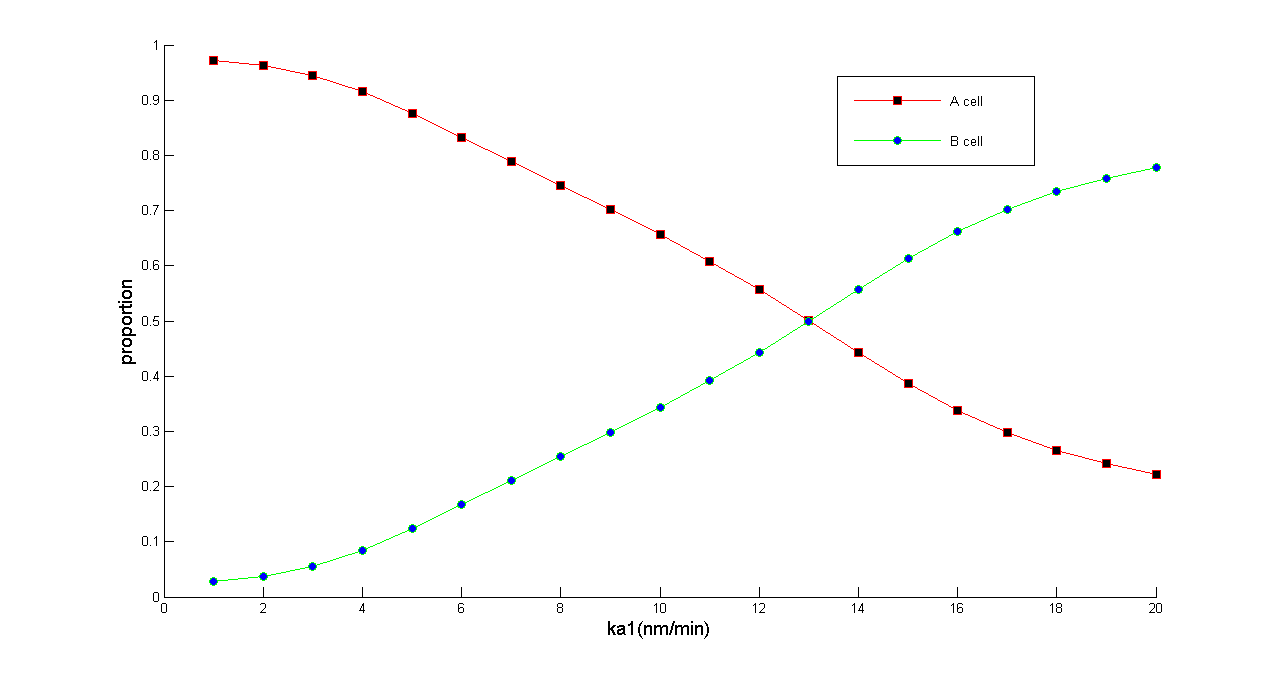
An ordinary differential equation (ODE) model was built to simulate population behaviors of our system. The results predicted that our population dynamic balancer can control A(B) cell with arbitrary proportion and the whole system always gets to a steady state without oscillation. Click to check our model page for more information.


Proportion.png


Figure 5 Normalized dose-response curve from the ODE simulation. Ka1 stands for transcription rate of ptsG1 and Salicylate Generator. (in bench work, addition of thiamine pyrophosphate, TPP, can modulate this parameter) As Ka1 vary from 1-20 nmol•min^-1,the ratio of A & B cell populations may be arbitrarily modulated from 0.2 to 1


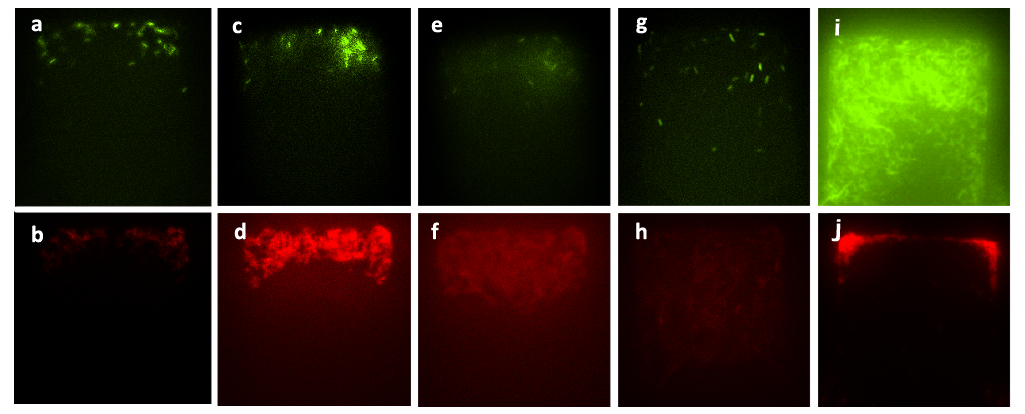
In terms of engineering communication with dedicated molecules, population behavior is much density-dependent unless the system spontaneously reaches homeostasis and the ability to maintain consortia with unsteady structure is challenged. Taken all these considerations, we designed a general microfluidic platform for cell-cell communication in chemostat. Our A&B cell co-culture showed tunable population ratio dynamics in our microfluidic device. Check the Microfluidic device page for more information.


PkusmfNo6.png


Figure 6. Figure (a) to Figure (h) show the growth of the mixed culture (A cells together with lasI-deficient B cells, referred to as ΔB cells) with inducer generated by CinI (with the initial concentration) inoculated in the upper layer (with the amplification factor of 20, the size of chambers 120μm×120μm, and the intruding velocity of 10μL/h). Photos were taken every one hour, and the time interval lasted three hours. A cells, which were indicated by GFP they expressed, did not grow during this time interval, while B. cells grew vigorously till they filled up the chamber. Figure (a) to Figure (h) illustrate the fact that the inducer generated by CinI could only repress the growth of A cells. Figure (i) and Figure (j) demonstrate the final state of this mixed culture’s growth with salicylate (with the concentration of 10^(-3) mol/L )inoculated in the upper layer, which acted as the inducer designed for inducing the expression of CcdB in ΔB cells( also with the amplification factor of 20, the size of chambers 120μm×120μm, and the intruding velocity of 10μL/h). cells. In this case, A cells finally filled up the chamber, while B. cells kept small population number after three hours’ cultivation.


PkusmfNo7.png


Figure 7. Figure (a_1) and (a_2) show the initial state of the mixed culture in the chamber, the number of A cells and that of ΔB cells were almost the same. Then we inoculated the mixture of salicylate with the concentration of 10^(-3) mol/L and the solution which was diluted in fold of 10^5 from the initial solution of inducer generated by CinI, the inducers for A cells and ΔB cells. Figure (b_1), (b_2), (c_1), (c_2), (d_1) and (d_2) show that the ratio of population number of A cells to that of B. cells had changed from the initial state and stayed the same during the two hours, which means that the culture came to a steady state under the control of inducers. Figure (e_1), (e_2), (f_1), (f_2), (g_1), (g_2), (h_1) and (h_2) illustrate the growth of the mixed culture with the mixture of salicylate with the concentration of 10^(-4) mol/L and the solution which was diluted with nutrient solution in fold of 10^4 from the initial solution of inducer generated by CinI. During this time interval, ΔB cells grew fast while A cells were extruded from chamber. In Figure (g_1) and (g_2), the number of ΔB cells decreased a little, mainly because the time-delayed effect of the control of salicylate, but the population soon recovered from the effect. Finally, in Figure (h_1) and (h_2), ΔB cells nearly filled up the whole chamber while there were few A cells in the same chamber.


To sum up, we featured our system with such specifications:

Multiple ‘chemical wires’ utilization

Multi-population interactions and signal integration

Tunable population behavior

Theoretical and physical device supporting

References

1．Brenner, K., You, L. C. & Arnold, F. H. Engineering microbial consortia: a new frontier in synthetic biology. Trends Biotechnol 26, 483-489 (2008)

2．Brenner K, Karig DK, Weiss R, Arnold FH (2007) Engineering bidirectional communication mediates a consensus in a microbial biofilm consortium. Proc Natl Acad Sci USA 104: 17300–17304

3．You, L., Cox, R. S. 3rd, Weiss, R. & Arnold, F. H. Programmed population control by cell–cell communication and regulated killing. Nature 428, 868–871 (2004).

4. Basu S, Gerchman Y, Collins CH, Arnold FH, Weiss R (2005) A synthetic multicellular system for programmed pattern formation. Nature 434: 1130–1134

5. Kerr, B., Riley, M., Feldman, M. & Bohannan, B. Local dispersal and interaction promote coexistence in a real life game of rock–paper–scissors. Nature 418, 171–174 (2002).

Top↑

Retrieved from "http://2011.igem.org/Team:Peking_S/project/nonb"