Team:Peking S/modeling/Result
From 2011.igem.org
(Created page with "_NOTOC__ {{Template:Http://2011.igem.org/Team:Peking_S/box4modeling}} <font color="#ffffff"><font size=6>Population Density Balancer</font> <font color="#000000"> {{Template...") |
(→Parameters) |
||
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | |||
{{Template:Http://2011.igem.org/Team:Peking_S/box4modeling}} | {{Template:Http://2011.igem.org/Team:Peking_S/box4modeling}} | ||
| Line 16: | Line 15: | ||
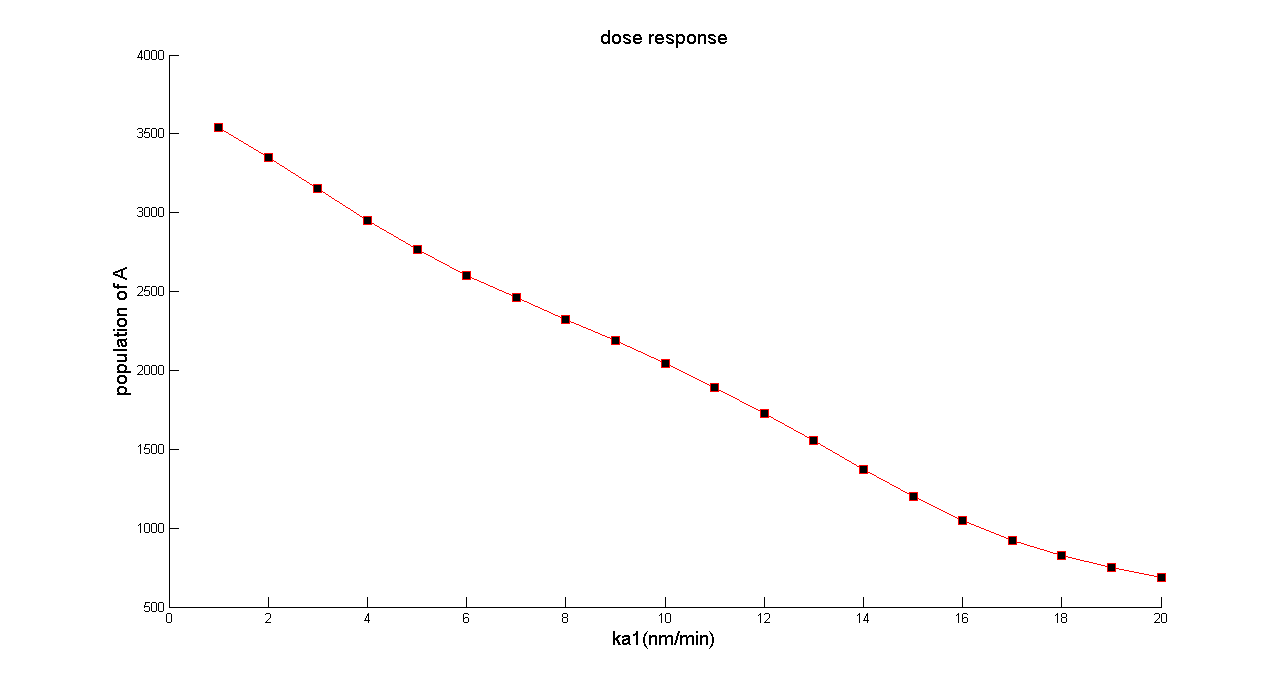
By varying the value of ka1 (in bench work, addition of thiamine pyrophosphate, TPP, can modulate this parameter), we can customize the population of A cell at steady state. | By varying the value of ka1 (in bench work, addition of thiamine pyrophosphate, TPP, can modulate this parameter), we can customize the population of A cell at steady state. | ||
| - | [[File: | + | [[File:Dose.png|650px|]] |
| + | ''Figure 3 the dose response. To testify whether our population density balancer can balance the population density with arbitrary ratio of two populations of cells, we simulated population of A cell separately with value of ka1 among a wide range. The figure shows the population of A cell at steady state can be modulated dramatically by parameter ka1. Beside, the correlation between the population of A cell and ka1 represents nearly linear, with linear correlation coefficient R=0.9973'' | ||
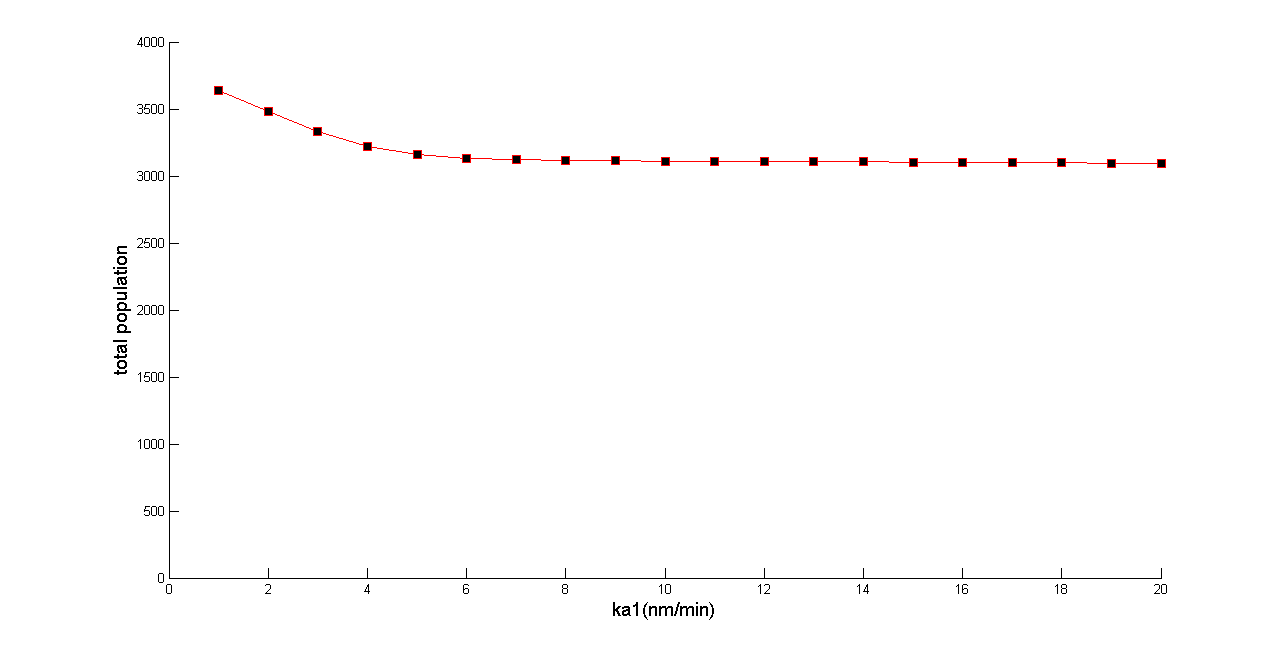
The total population (A and B) size is approximately equal to K, and only vary slightly along with the change of ka1. | The total population (A and B) size is approximately equal to K, and only vary slightly along with the change of ka1. | ||
| - | [[File: | + | [[File:Fjc.png|650px]] |
| + | |||
| + | ''Figure 4 The variation of total population size (A and B cell) at steady state along with the change of ka1’s value. The result confirms that the total population is unrelated to the value of ka1 tightly and we can regard it as a constant.'' | ||
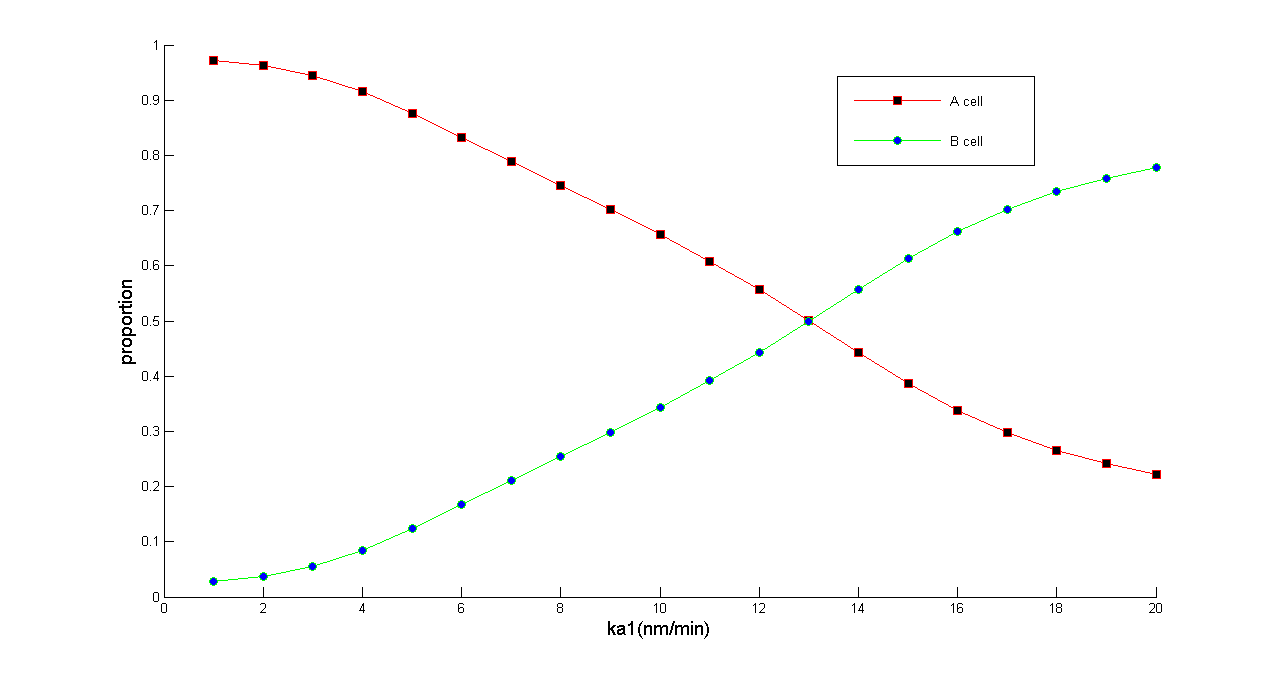
Hence the proportion of A(B) cell can be changed significantly: | Hence the proportion of A(B) cell can be changed significantly: | ||
| - | [[File: | + | [[File:Proportion.png|650px]] |
| - | Figure 5 Normalized dose response curve. We redraw figure 3 after normalizing population. This figure proves that we can balance the population of A and B cell with arbitrary ratio from 0.2 to1 | + | |
| + | ''Figure 5 Normalized dose response curve. We redraw figure 3 after normalizing population. This figure proves that we can balance the population of A and B cell with arbitrary ratio from 0.2 to1'' | ||
In summay, our model predicted that it is very possible to efficiently modulate the ratio of A cell/B cell for its wide working range by tuning the transcriptional rate of mRNA 1 . | In summay, our model predicted that it is very possible to efficiently modulate the ratio of A cell/B cell for its wide working range by tuning the transcriptional rate of mRNA 1 . | ||
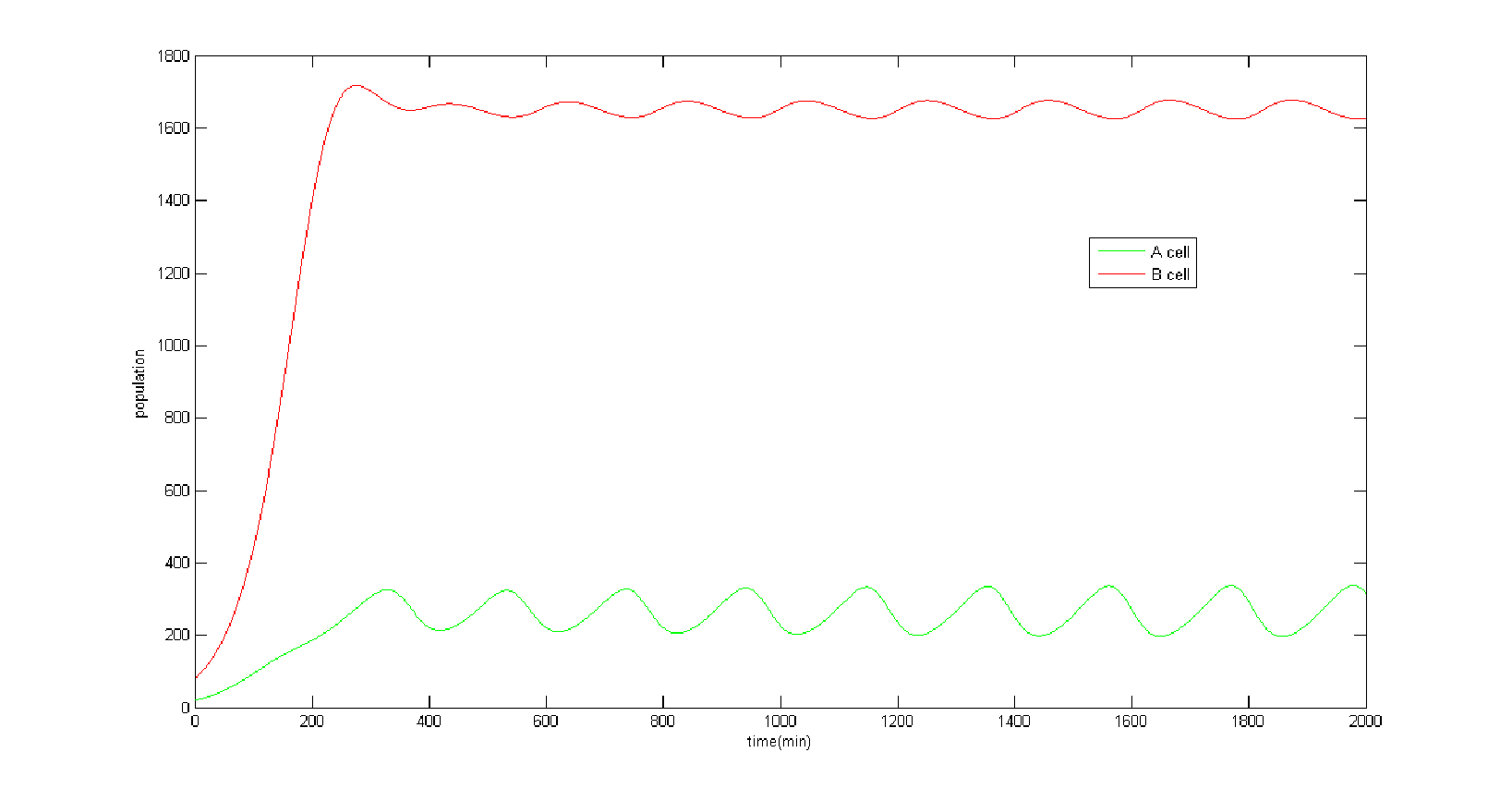
We wondered whether our model could produce oscillation under certain parameter selection. The oscillation is interesting, in which the population of A and B cell can’t get balanced and will vary from time to time. Intuitively, we expected the system to become an oscillator, for there exist the necessary feedback loops for oscillation. However, we only find 6 sets of parameters in 100,000 that can produce oscillation and the amplitude of the oscillation is quite small compared with total population. (Figure 6) | We wondered whether our model could produce oscillation under certain parameter selection. The oscillation is interesting, in which the population of A and B cell can’t get balanced and will vary from time to time. Intuitively, we expected the system to become an oscillator, for there exist the necessary feedback loops for oscillation. However, we only find 6 sets of parameters in 100,000 that can produce oscillation and the amplitude of the oscillation is quite small compared with total population. (Figure 6) | ||
| + | [[File:PkumoreFigure6.png|650px]] | ||
| - | + | ''Figure 6 Oscillation with small amplitude This figure exhibits the simulation result under the parameters which can cause oscillation. We must point out such parameters are rare and can hardly be met. It is also notable that the amplitude of oscillation is quite small so we can approximately regard the system as getting to a steady state instead of limited cycle, which means our balancer can work normally.'' | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | Figure 6 Oscillation with small amplitude This figure exhibits the simulation result under the parameters which can cause oscillation. We must point out such parameters are rare and can hardly be met. It is also notable that the amplitude of oscillation is quite small so we can approximately regard the system as getting to a steady state instead of limited cycle, which means our balancer can work normally. | + | |
| - | + | ||
| - | + | ||
| + | The probability of appearing oscillation is tiny because the parameter sets causing oscillation is rare. Hence there is no need to worry that unexpected oscillation will disturb the performance of our population dynamic balancer. | ||
| - | |||
| + | In summary, our population density balancer can constrain the population of A (B) cell in arbitrary proportion. And the whole system is robust enough to perform as population balancer with minimal possibility as an oscillator. Besides, we can expect that the topology of our system is capable of balancing cell population while the ratio of A/B cell can be still tuned among a wide range. | ||
===Reference=== | ===Reference=== | ||
| - | [1] | + | [1] Maki.S, Takiguchi.S, Miki.T, and Horiuchi.T. Modulation of DNA Supercoiling Activity of Escherichia coli DNA Gyrase by F Plasmid Proteins THE JOURNAL OF BIOLOGICAL CHEMISTRY 267 No. 17.12244-12251,(1992) |
| - | [2] | + | [2] Levine.E, Zhang.Z, Kuhlman.T, Hwa.T. Quantitative Characteristics of Gene Regulation by Small RNA. PLoS Biology 5.9-e229(2007). |
| - | [3] | + | [3] Tamsir.A, Tabor.J & Voigt.C.A. Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’.NATURE 469.212(2011) |
Latest revision as of 02:56, 6 October 2011
Template:Https://2011.igem.org/Team:Peking S/bannerhidden

Population Density Balancer
ODEs|Parameters|Result
Parameters
By varying the value of ka1 (in bench work, addition of thiamine pyrophosphate, TPP, can modulate this parameter), we can customize the population of A cell at steady state.
Figure 3 the dose response. To testify whether our population density balancer can balance the population density with arbitrary ratio of two populations of cells, we simulated population of A cell separately with value of ka1 among a wide range. The figure shows the population of A cell at steady state can be modulated dramatically by parameter ka1. Beside, the correlation between the population of A cell and ka1 represents nearly linear, with linear correlation coefficient R=0.9973
The total population (A and B) size is approximately equal to K, and only vary slightly along with the change of ka1.
Figure 4 The variation of total population size (A and B cell) at steady state along with the change of ka1’s value. The result confirms that the total population is unrelated to the value of ka1 tightly and we can regard it as a constant.
Hence the proportion of A(B) cell can be changed significantly:
Figure 5 Normalized dose response curve. We redraw figure 3 after normalizing population. This figure proves that we can balance the population of A and B cell with arbitrary ratio from 0.2 to1
In summay, our model predicted that it is very possible to efficiently modulate the ratio of A cell/B cell for its wide working range by tuning the transcriptional rate of mRNA 1 . We wondered whether our model could produce oscillation under certain parameter selection. The oscillation is interesting, in which the population of A and B cell can’t get balanced and will vary from time to time. Intuitively, we expected the system to become an oscillator, for there exist the necessary feedback loops for oscillation. However, we only find 6 sets of parameters in 100,000 that can produce oscillation and the amplitude of the oscillation is quite small compared with total population. (Figure 6)
Figure 6 Oscillation with small amplitude This figure exhibits the simulation result under the parameters which can cause oscillation. We must point out such parameters are rare and can hardly be met. It is also notable that the amplitude of oscillation is quite small so we can approximately regard the system as getting to a steady state instead of limited cycle, which means our balancer can work normally.
The probability of appearing oscillation is tiny because the parameter sets causing oscillation is rare. Hence there is no need to worry that unexpected oscillation will disturb the performance of our population dynamic balancer.
In summary, our population density balancer can constrain the population of A (B) cell in arbitrary proportion. And the whole system is robust enough to perform as population balancer with minimal possibility as an oscillator. Besides, we can expect that the topology of our system is capable of balancing cell population while the ratio of A/B cell can be still tuned among a wide range.
Reference
[1] Maki.S, Takiguchi.S, Miki.T, and Horiuchi.T. Modulation of DNA Supercoiling Activity of Escherichia coli DNA Gyrase by F Plasmid Proteins THE JOURNAL OF BIOLOGICAL CHEMISTRY 267 No. 17.12244-12251,(1992)
[2] Levine.E, Zhang.Z, Kuhlman.T, Hwa.T. Quantitative Characteristics of Gene Regulation by Small RNA. PLoS Biology 5.9-e229(2007).
[3] Tamsir.A, Tabor.J & Voigt.C.A. Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’.NATURE 469.212(2011)
 "
"