Team:Wageningen UR/Project/ModelingProj1
From 2011.igem.org
(→Modeling synchronized oscillations) |
(→Modeling synchronized oscillations) |
||
| (38 intermediate revisions not shown) | |||
| Line 27: | Line 27: | ||
{{:Team:Wageningen_UR/Templates/NavigationLeft}} | {{:Team:Wageningen_UR/Templates/NavigationLeft}} | ||
{{:Team:Wageningen_UR/Templates/Style | text= __NOTOC__ | {{:Team:Wageningen_UR/Templates/Style | text= __NOTOC__ | ||
| + | === Mathematical model === | ||
| + | Since our BioBricked oscillatory system is based on the circuit published by Danino et al. in the paper “A synchronized quorum of genetic clocks” [1], our first model of the system is a reproduction of the mathematical model in the supplementary information [2] accompanying the mentioned publication. In their simulations, Danino et al. used a set of four delay differential equations, which we also used as starting point for our modeling work. | ||
| - | + | The steps (transcription, translation, maturation etc.) from the luxI and aiiA genes to the corresponding proteins are not modeled separately. Instead, the delay of the correlation between the internal AHL concentration, which triggers the expression of the genes, and the corresponding AiiA and LuxI concentrations is simulated by a Hill function. This Hill function takes the history of the system into account, i.e. the concentration of AHL at the time it binds to LuxR to form the activation complex. | |
| - | + | ||
| - | + | The experimental setup of the cited paper involved the use of microfluidic devices, in which the cell density could be kept constant. Excess cells were flushed away with a predefined flow rate. This also controlled the external AHL concentration. More information can be found in the description about the [[Team:Wageningen_UR/Project/DevicesSetup| setup]] of the device. | |
| - | [[ | + | [[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] |
| - | |||
| - | + | === Writing a modeling tool in Matlab === | |
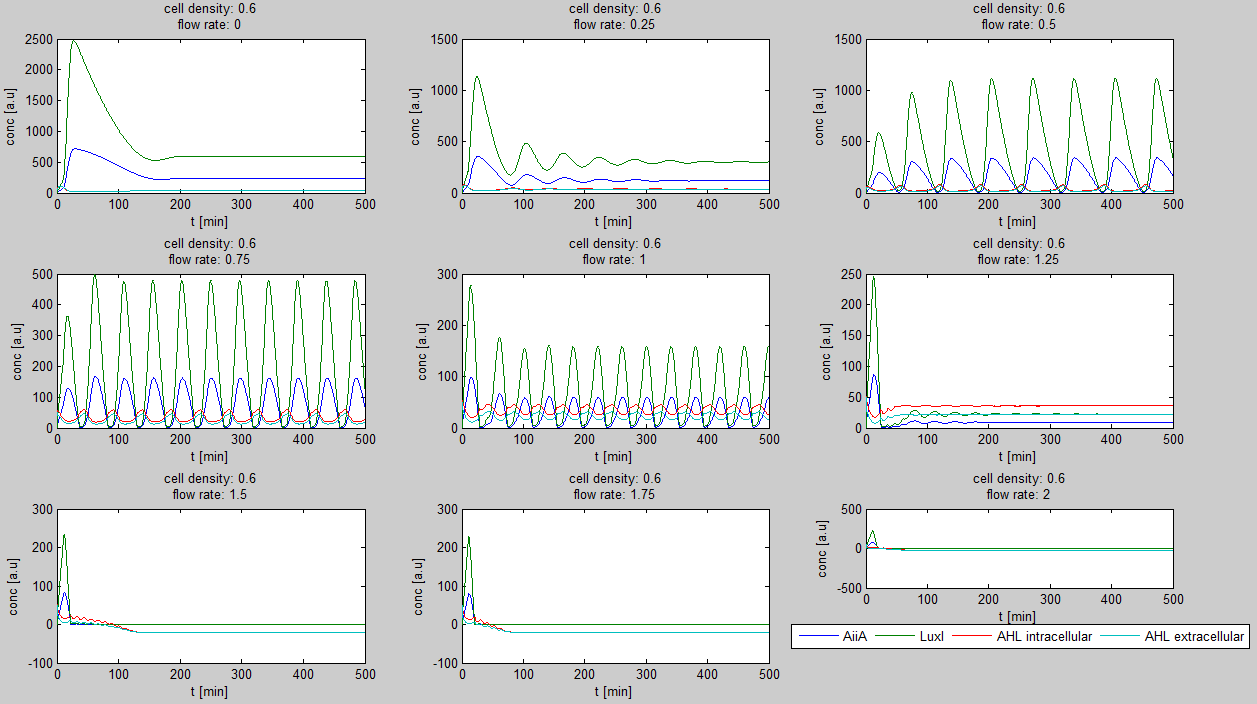
| + | For the first simulations, the same parameters were used as in the cited paper, the only variables thus being the cell density and flow rate. To get an idea about the different conditions in which oscillations could occur, our team created a script for a Matlab modeling tool which uses nested for-loops to vary the flow rate and cell density over a range of values. The resulting tool allows the user to enter the range in which the variables should be varied. The script then iterates over the values and plots graphs of all combinations possible for that range of values. Figure 2 shows an example output of the script. | ||
| + | |||
| + | |||
| + | [[File:Example_output_graphs_WUR.png|770px|center]] | ||
| + | |||
| + | '''Fig.1:''' ''Variation of output graphs depending on the different starting conditions'' | ||
| Line 44: | Line 50: | ||
[[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] | [[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] | ||
| - | |||
| - | === | + | === Preliminary conclusions for our system === |
| + | The first observation from the model was that for oscillations to occur, the flow rates may not be too fast. This especially holds at low cell densities (see output graphs above). Since the device used for our system has larger dimensions than the microfluidic device used by Danino et al. the flow rates required could not be achieved by varying height differences alone. <!-- Further information can be found in the information about the [[Team:Wageningen_UR/Project/Devices#Setup| platform used to measure oscillations.]] --> | ||
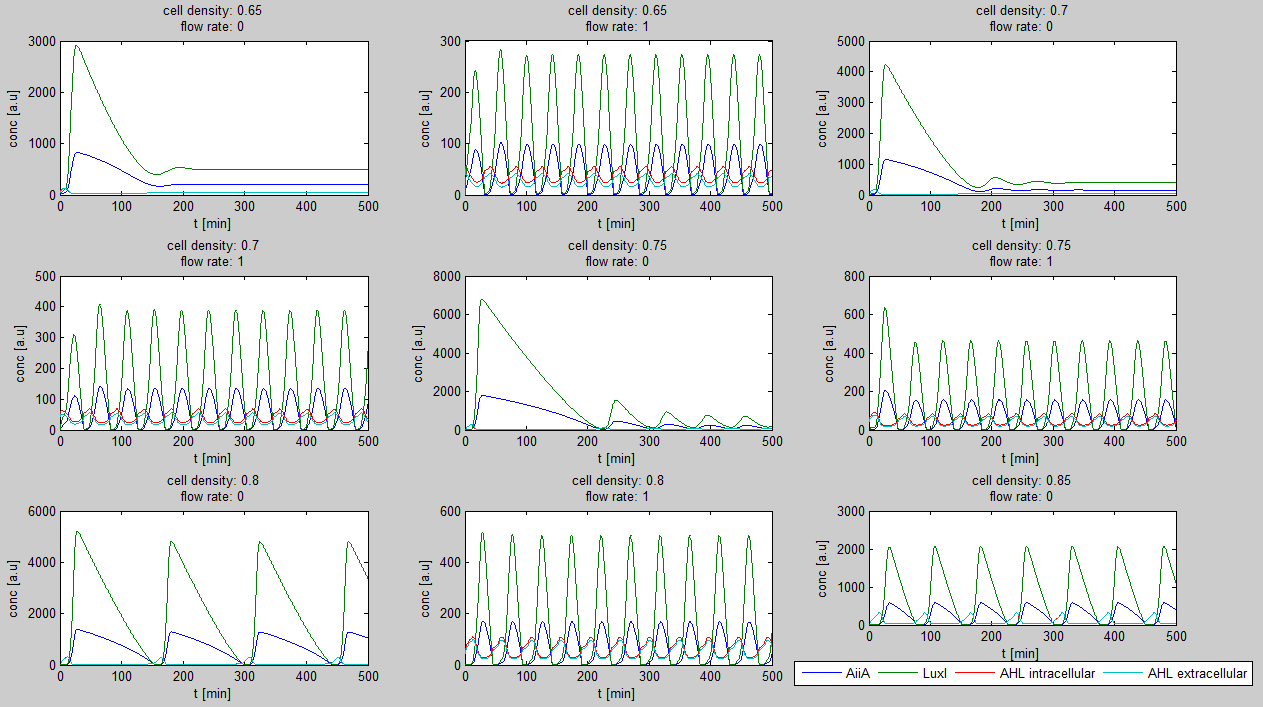
| - | + | Furthermore, an interesting observation was that applying a flow rate over the cells was not essential to obtain oscillations. Figure 3 shows how - according to the model - oscillations can potentially occur at 0 flow rate. Interesting is that this happens only at high cell densities. | |
| - | + | ||
| - | + | ||
| + | [[File:Model0flow_WUR.png|770px|center]] | ||
| - | ''' | + | '''Fig.2:''' ''Graphs showing oscillatory behavior increasing with cell density even when the flow rate is set to 0'' |
| - | + | Disregarding the strictly mathematical model, some more conclusions were drawn from modeling work as to whether to use a microdish or microsieve as platform for measuring oscillations. This is described in more detail in the [[Team:Wageningen_UR/Project/DevicesSetup| section about the setup of the device.]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | |||
| - | + | [[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] | |
| + | === Expansion of the model for the double tunable oscillatory construct === | ||
| + | To model the [[Team:Wageningen_UR/Project/CompleteProject1Description#3._Designs| double tunable oscillator]], the original set of delay differential equations [2] was expanded. This involved adding the effect of the repressor and activator in the form of a Hill function to the differential equations for LuxI and AiiA. The equations for the internal and external AHL concentrations were not changed. The new set of equations is depicted below. | ||
| - | + | [[File:Equations_enhanced_WUR.png]] | |
| + | '''Fig.3''' ''Adjusted set of differential equations for the double tunable oscillator'' | ||
| + | Since the LacI repressed hybrid promoter used for this system was designed by the Tokyo iGEM 2007 team [3], the additional terms were derived according to their model. The tetR repressor was then modeled using the same template. The set of equations seen above therefore integrates the features of both models. It does not include differential equations for LuxR, LacI (represses luxI) and tetR (represses aiiA). For the model we assume that these proteins are constitutively produced. | ||
| - | in | + | The equations suggest slowing down of protein synthesis at higher cell densities d (first term in the LuxI (eq 1) and AiiA (eq2) equations). The Hill function including a tau describes the delayed production of AiiA and LuxI depending on the internal AHL concentration at a past time point, as explained above. Gamma represents the degradation rate of the respective proteins. LuxI produces AHL, this dependency is shown in the first term of the differential equation for the internal AHL concentration (eq3). The terms proportional to D show the diffusion of AHL into and out of the cell. The flow rate mu, which removes external AHL, is only relevant when actually applying flow and is set to 0 for most of our simulations. [1] |
| - | + | The terms which were added to the original set of equations showing the influence of the repressor and activator are highlighted below. | |
| - | [[ | + | [[File :Equations_enhanced_highlighted_WUR.png]] |
| + | The parameters of these terms were roughly estimated, and are not yet confirmed. The other parameters were experimentally determined by Danino et al. and the values can be found in their supplementary information [2]. | ||
| - | |||
| - | |||
| - | |||
| - | + | [[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] | |
| - | |||
| + | === Writing a new modeling tool for the Synchroscillator === | ||
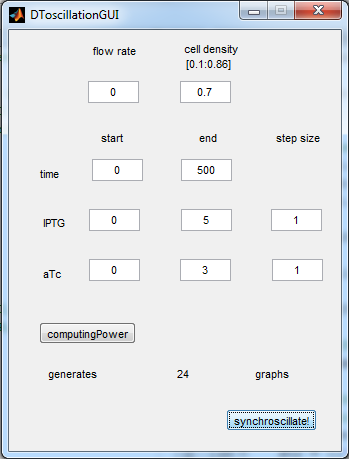
| + | The new equations were used to write another Matlab modeling tool, of which the GUI is depicted below. | ||
| - | [[File: | + | [[File:GUI_2_synchroscillator_WUR.png|300px|center]] |
| + | '''Fig.5''' ''Revised GUI for the Synchroscillator'' | ||
| - | |||
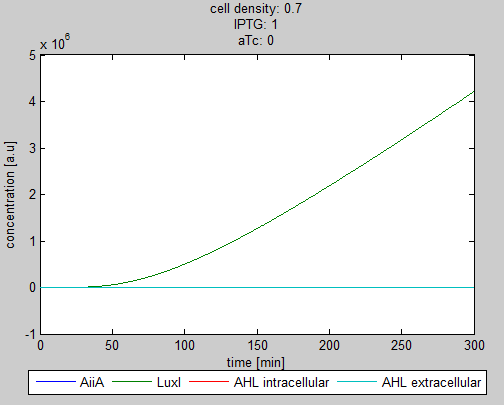
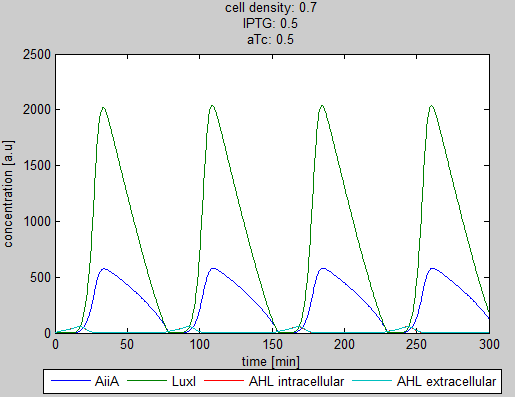
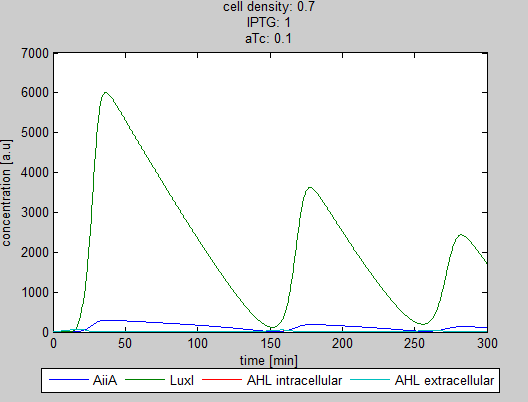
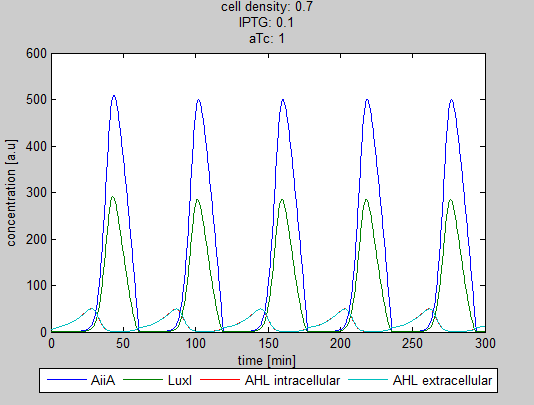
| + | As can be seen in the GUI, the new model allows the construct to be controlled by changing the concentrations of IPTG and aTc. Since the parameters could not be verified by wet lab experiments yet, some example conditions were simulated of which the output graphs are seen below. | ||
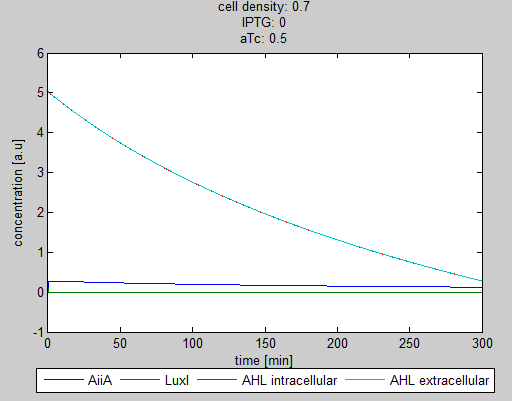
| + | [[File:Graph1_2_synchroscillator_WUR.png|center]] | ||
| - | |||
| + | '''Situation 1:''' ''Only aTc, no IPTG. Some AiiA can be produced, but no production of LuxI, since it is fully repressed by LacI. As a result all AHL is degraded.'' | ||
| - | |||
| - | + | [[File:Graph3_2_synchroscillator_WUR.png|center]] | |
| - | |||
| - | + | '''Situation 2:''' ''Only IPTG, no aTc. LuxI and as a result internal AHL (red curve hidden under green curve) is produced. The production of AiiA is fully repressed.'' | |
| - | |||
| - | + | [[File:Graph2_2_synchroscillator_WUR.png|center]] | |
| - | + | '''Situation 3:''' ''Equal amounts of IPTG and aTc produce oscillations as seen in previous simulations.'' | |
| - | |||
| - | + | [[File:Graph4_2_synchroscillator_WUR.png|380px]] [[File:Graph5_2_synchroscillator_WUR.png|380px]] | |
| - | |||
| + | '''Situation 4 and 5:''' ''Interesting behavior of the system when adding IPTG and aTc in reversed proportions.'' | ||
| + | |||
| + | From the model it can be concluded that the oscillatory behavior can indeed be fine tuned. However, wet-lab experiments are needed to quantify the parameters. | ||
| + | |||
| + | |||
| + | |||
[[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] | [[Team:Wageningen_UR/Project/ModelingProj1#Modeling_synchronized_oscillations| back to top]] | ||
| + | |||
| + | '''Links and references:''' | ||
| + | |||
| + | [1][http://www.nature.com/nature/journal/v463/n7279/abs/nature08753.html Danino et al. 2010] | ||
| + | |||
| + | [2][http://www.nature.com/nature/journal/v463/n7279/suppinfo/nature08753.html Supplementary information] | ||
| + | |||
| + | [3][https://2007.igem.org/Tokyo/Works Tokyo iGEM 2007] | ||
| + | |||
| + | |||
}} | }} | ||
Latest revision as of 03:31, 22 September 2011
 "
"