Team:Paris Bettencourt/Modeling
From 2011.igem.org

Modeling introduction
What is modeling in synthetic biology?
Synthetic biology relies heavily on genetic constructs designed to perform a specific task. In order to predict the behaviour of such systems, we need to be able to model it. Knowing in advance how well or how poorly a construct will work can help us during the genetic design phase or the preparation of our experiments. We need to describe the future reactions of our system by creating a mathematical model of it. The parameters of the model are then fitted to the experimental results.
The bible for synthetic biology modeling is Uri Alon's book An Introduction to Systems Biology: Design Principles of Biological Circuits [1]. Most of our models are based on his approach to biological circuits. We are now going to explain quickly what is the basic structure behind our simulations.
The gene ''geneX'' is responsible for the production of the corresponding protein X. The promoter pX controlling the expression geneX can be:
- A constitutive promoter, geneX is activated whatever the conditions
- Positively regulated, geneX is more active when an inducer is present
- Negatively regulated, geneX is less active when an repressor is present

Constitutive promoter

Positive autoregulation

Negative autoregulation
The inducer or repressor can be another protein or even the product itself. In the latter case, the gene is auto-regulated, wether positively or negatively. To begin, let's assume pX is a constitutive promoter for now. We will make another simplification by taking into account the translation step and assuming that the gene "directly" produces protein X.
We will know take a look at the parameters involved in modeling this network.
- [X] is the concentration of protein X
 is the expression rate of protein X (molecule.s-1). It mainly depends on the constitutive promoter.
is the expression rate of protein X (molecule.s-1). It mainly depends on the constitutive promoter. is the dilution rate, due to cell division (s-1)
is the dilution rate, due to cell division (s-1) is the degradation rate of protein X (s-1)
is the degradation rate of protein X (s-1)
The equation and solution modeling the behaviour of this system are the following:
Constitutive expression of protein X over time
Now, let's assume that pX is auto-regulated, either positively or negatively. We need to introduce a few new parameters.
- K is the dissociation constant, representing the binding of a inducer/repressor to the promoter
- n is the Hill coefficient of the function
 is the maximum production rate of our gene (molecule.s-1)
is the maximum production rate of our gene (molecule.s-1) now represents the basal expression ("leaking") of the gene (molecule.s-1)
now represents the basal expression ("leaking") of the gene (molecule.s-1)
The constants used in our examples below are arbitrary and chosen to amplify the behaviours expected. The equations and solutions are now:
Positive autoregulation equation and behaviour
Negative autoregulation equation and behaviour
You will note that the regulation is modeled as a Hill function. This type of function is used to represent most of the regulation that takes place in a genetic network.
Of course most genetic networks are more complex than simply auto-regulated nodes. The product of one gene can regulate the activation of another which in turn inhibits a third, etc. By coupling this kind of equations together, we achieved modeling most of our genetic networks pretty easily.
Our choices for modeling
Steady state flow from the nanotubes
A lot of our designs are based on a simple emitter cell - nanotubes - receiver cell principle. The basic models however can not take into account the nanotubes transfer. We decided to make separate models for particles transmission through the nanotubes and to assume that the number of signaling protein going through them reaches a "steady state" in the receiver cell. It can be reached when the flow through nanotubes into the cell exactly compensate protein degradation and dilution. The reason for such a choice is to simplify the interpretation of data. If we were using a non-steady flow of signaling protein, understanding the behaviour of our reporters would have been much more difficult.
The way we present our models is the following. We first model both emitting and receiving genes in the same cell to give us a control. We then see what would be the response of the receiver genes alone in a cell for different signaling protein steady states. We can then compare our models to reality and evaluate the influence of nanotubes on the response of the system.
Translation
We introduced the translation step in our models. This means each equation described above is transformed into two equations: one describing mRNA production and one describing the translation of this mRNA into a protein. We then need to introduce the protein production rate  (s-1). We also need to introduce a different degradation rate for each product. The first one will be for the degradation of mRNA associated with geneX and the second one with protein X itself. The equations for the auto-repression (other regulation systems are similar) are now:
(s-1). We also need to introduce a different degradation rate for each product. The first one will be for the degradation of mRNA associated with geneX and the second one with protein X itself. The equations for the auto-repression (other regulation systems are similar) are now:

This is justified notably because of our tRNA construction. This design relies directly on the translation process, we therefore need to model it if we want to compare models for different designs.
Delays for maturation
We also introduced a delay for protein production and maturation. Most models can ignore this but our experiments rely heavily on time measurements which means that for proteins with maturation time around 5 min (to compare with the cell division time 40 min) we need to take this into account. We chose to model this simply by adding a delay to the response time as it is shown in the following equations:

The delay for mRNA production is significantly lower than the one for protein production:  <<
<<  .
.
No delays for diffusion in receptor cell
Most of our designs rely on the following scheme: an emitter cell creates a signaling protein which is received through the nanotubes by a receiver cell which is then activated. However, one could argue that after entering the receiver cell, the signaling proteins spend a significant time diffusing in it before reaching the receptor gene construct. We discussed this at length before finally agreeing not to consider this as a delay.
Several models showed us that diffusion, even of a single signaling molecule, happen too fast to add any delay to the response time of the system. We will discuss two of these models here.
Using diffusion equations
The first step is to study the general principles of diffusion and to apply them to a single molecule. We expected to estimate the order of magnitude for diffusion time of molecules with this model, not to have a precise understanding of the movement of molecules in a cell. Most of our experimental designs rely on time measurement to characterize the nanotubes, it was therefore crucial to see if diffusion time could add a significant delay to the response of receiver cells.
The principle of this model is quite simple. We use the statistical diffusion equation with a new normalization constant so that it describes the behaviour of one molecule. Rather than obtaining a concentration field, we end up with a distribution of the density of probability to find the molecule at a certain position and a certain time. We did not use any kind of boundary conditions, we therefore only model the "movements" of one molecule floating in an infinite water medium.
The equation of diffusion is the following:

Where c is the concentration of particles in the cell, function of  (position) and t (time). D is the diffusion coefficient.
(position) and t (time). D is the diffusion coefficient.
We decided to use as initial conditions a Dirac function centered on the origin of space. The solution for such an equation is:

This solution shows that through time, the density of probability "diffuses" in all directions equally. So we have take advantage of the spherical symetry of the problem.


(Note that this serie of graph is here only as an example. The units are arbitrary.)
What is of interest for us is the instant when we can consider that the probability of presence of the molecule is "the same" for every point in the cell. The cell here is an arbitrary boundary which has no direct impact on the model. In our approach, the cell is a sphere centered on the origin and with a diameter of 1 micrometer (roughly Subtilis length). We chose to consider that the probability is "the same" when the lowest probability within the cell is 95% of the highest probability in the cell (i.e. in the center).
We can then solve analytically the equation. Let us call  the time when the probability is the same (at 95%) within the cell boundaries. This means that for concentration for x=cell radius is 0.95 times concentration for x=0.
the time when the probability is the same (at 95%) within the cell boundaries. This means that for concentration for x=cell radius is 0.95 times concentration for x=0.
You will find in the table below a list of such characteristic times for different molecules.

Using a stochastic model
This model is very similar to the one used in [Ribosome kinetics and aa-tRNA competition determine rate and fidelity of peptide synthesis. Fluitt A, Pienaar E, Viljoen H. Comput Biol Chem. 2007 Oct;31(5-6):335-46. Epub 2007 Aug 15.]. We consider that the particle diffusing in the cell is a random walker.
We want to see how long it takes for a particle of a given size to diffuse to any point of a cell. We use the following parameters:
- V volume of the cell (10-18 m3)
 characteristic size of the particle (m)
characteristic size of the particle (m)- D diffusion coefficient of the particle (m2.s-1)
We divide the cytoplasm volume V into  occupation sites for the walker. The characteristic time
occupation sites for the walker. The characteristic time  associated with the transition from one site to another is:
associated with the transition from one site to another is: [http://www.ece.gatech.edu/research/labs/bwn/papers/2011/c6.pdf]
[http://www.ece.gatech.edu/research/labs/bwn/papers/2011/c6.pdf]
If we have R walkers of this type, the probability that a molecule arrives at a given occupation site during the time interval  is:
is:  . In our case we study only one molecule (worst case scenario) so let us assume R=1.
. In our case we study only one molecule (worst case scenario) so let us assume R=1.
The average time that elapses before the arrival of a particle is:  .
.
You will find below a table of time before arrival for different molecules.

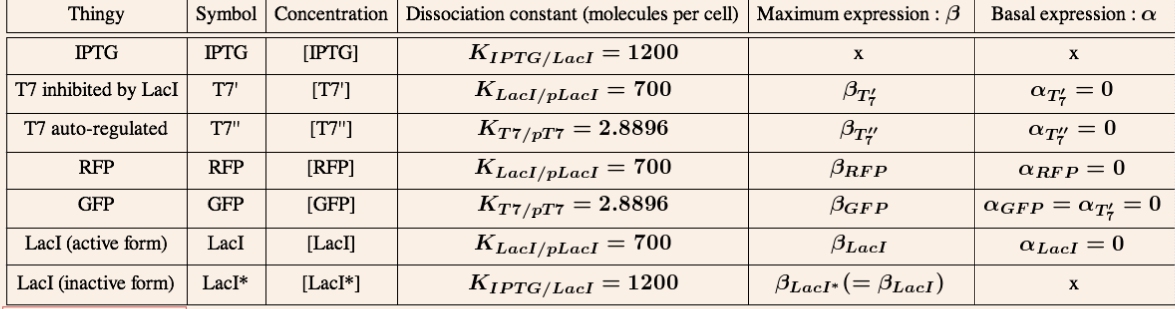
Parameters
Finally, we made some assumptions for certain parameters that are used in most of our models. These assumptions are discussed at length in the parameters section.
References
- Test
- Re-Test
Contents |
Direct observation
Characterization
T7 system
tRNA_amber system
Distribution of tRNA_amber in mRNA populations
Master/Slave
Bi-directional communication
 "
"