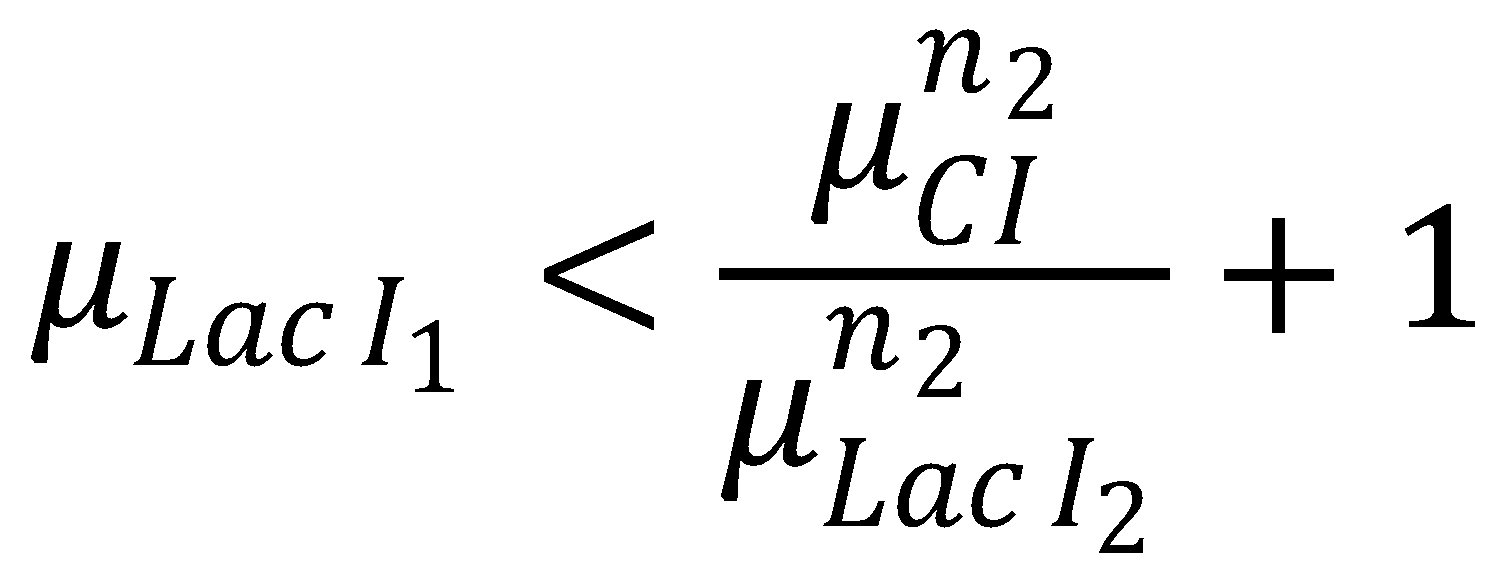|
|
| Line 1: |
Line 1: |
| - | {{:Team:ETH Zurich/Templates/HeaderNew}}
| |
| - |
| |
| - | {{:Team:ETH Zurich/Templates/SectionStart}}
| |
| - | = Analytical Approximation =
| |
| - | {{:Team:ETH Zurich/Templates/SectionEnd}}
| |
| - |
| |
| - | {{:Team:ETH Zurich/Templates/SectionStart}}
| |
| - |
| |
| - | = Steady State Gradient Approximation =
| |
| - | We derived the gradient formation dynamics analytically already in the [[Team:ETH_Zurich/Modeling/Microfluidics#Model|reaction-diffusion model]]. However, there we only solved the resulting partial differential equation numerically. '''Here, we are going to venture forth and give a suitable analytical approximation!'''
| |
| - | == Kolmogorov-Petrovsky-Piskounov Equation ==
| |
| - | In mathematics, the problem posed by general reaction-diffusion systems form is known as the '''Kolmogorov-Petrovsky-Piskounov Equation'''. In the case of acetaldehyde as diffusing and reacting molecule, the equation has the following general structure:
| |
| - | [[File:ETH-AcAl-Reaction-Diffusion.png|317px|center|thumb|'''General Kolmogorov-Petrovsky-Piskounov partial differential equation''' for an acetaldehyde-based reaction-diffusion system. '''D(AcAl(x,z),z)''' is the diffusive term, '''R(AcAl(x,z))''' is the uniform (independent of the spatial z coordinate) reaction term.]]
| |
| - |
| |
| - |
| |
| - | In our case, it has the following, less general form we already derived analytically for [[Team:ETH_Zurich/Modeling/Microfluidics#Model|the reaction-diffusion model for acetaldehyde]]: [[File:ETHZ-AcAl-Diffusion-Degradation.png|573px|center|thumb|'''Kolmogorov-Petrovsky-Piskounov partial differential equation''' for our system, as derived in [[Team:ETH_Zurich/Modeling/Microfluidics#Model|the reaction-diffusion model for acetaldehyde]].]]
| |
| - |
| |
| - | <html><h3></html> Boundary Conditions <html></h3></html>
| |
| - | For the analytical approximation of the acetaldehyde gradient, we only consider the boundary condition that the concentration at the reservoir (located at z = 0) stays constant:
| |
| - |
| |
| - | [[File:ETHZ-BoundaryCondition-Reservoir.png|center|206px|thumb|[http://en.wikipedia.org/wiki/Dirichlet_boundary_condition Dirichlet Boundary Condition] for the concentration of acetaldehyde at the reservoir]]
| |
| - |
| |
| - | This is in contrast to the full model, where we enforce that no diffusion occurs through the opening at the side of the channel which is closed and not connected to the reservoir. However, we will see that for our circuit, this assumption is valid as long as we are inside the detection range of our circuit, which is the case that we are interested in. In the end, we can also detect if we go out of detection range in the analytical model and make sure this assumption holds.
| |
| - |
| |
| - | == Solution at Steady State ==
| |
| - | At steady state, we have to solve the KPP equation for the time derivative set to zero, i.e.
| |
| - |
| |
| - | [[File:ETHZ-KPP-SteadyState.png|thumb|center|565px|Steady-State Kolmogorov-Petrovsky-Piskounov (KPP) Equation]]
| |
| - |
| |
| - | === 1. Simplification ===
| |
| - | Before we get started with solving the actual equation, we simplify it by gathering all the parameters we can:
| |
| - |
| |
| - | [[File:ETHZ-KPP-Simple.png|thumb|center|321px|Simplified parameters]]
| |
| - |
| |
| - | [[File:ETHZ-KPP-SteadyState-Simple.png|thumb|center|407px|Simplified Steady-State Kolmogorov-Petrovsky-Piskounov (KPP) Equation]]
| |
| - |
| |
| - | === 2. Approximation ===
| |
| - | Next, we assume that the Michaelis-Menten-type degradation in our KPP operates at or almost at saturation for the relevant part of the gradient. This assumption holds for inputs that are within detection range according to the exact numerical integration of the KPP equation.
| |
| - |
| |
| - |
| |
| - | This means we can approximate the reaction term around saturation, i.e. AcAl*(z) >> K<sub>M,AcAl</sub>:
| |
| - |
| |
| - | [[File:ETHZ-KPP-Saturation-Approximation.png|thumb|center|185px|Saturation approximation of the reaction term for AcAl*(z) >> K<sub>M,AcAl</sub>]]
| |
| - |
| |
| - |
| |
| - | We have now arrived at a '''solvable ordinary differential equation''' for the acetaldehyde gradient:
| |
| - | [[File:ETHZ-KPP-Approx-ODE.png|thumb|center|507px|Ordinary Differential Equation approximation for acetaldehyde gradient at steady state]]
| |
| - |
| |
| - | === 3. Partial Analytical Solution ===
| |
| - | We can solve the ordinary differential equation we derived before by integrating wrt. to z twice, thereby introducing an unknown integration constant κ:
| |
| - | [[File:ETHZ-KPP-Approx-ODE-PartialSol.png|365px|center|thumb|Parital solution with open parameter κ to the ordinary differential equation arising from the KPP equation.]]
| |
| - | In the approximate solution to the problem, negative concentrations might be obtained due to the presence of the zeroth-order term in the KPP partial differential equation. '''To determine κ and avoid negative concentrations in the approximate solution, we apply the dead-zone concept.'''
| |
| - |
| |
| - |
| |
| - |
| |
| - | == Dead Zone Concept ==
| |
| - | The dead zone concept introduces a nonreaction zone. It is an approximation to the Kolmogorov-Petrovsky-Piskounov equation for saturation of Michaelis-Menten kinetics that tends to work better than the orginial boundary conditions [[#Ref1|[1]]]. In our case, for the nonreaction zone, we require that
| |
| - | * no reactant, i.e. acetaldehyde, is present: <br />[[File:ETHZ-KPP-DeadZone-I.png|176px]]
| |
| - |
| |
| - |
| |
| - | * no diffusion occurs across the dead zone: <br />[[File:ETHZ-KPP-DeadZone-II.png|221px]]
| |
| - |
| |
| - |
| |
| - | The solution to the problem posed by the ODE steady-state approximation of the Kolmogorov-Petrovsky-Piskounov equation and the dead-zone concept gives a value for κ:
| |
| - | [[File:ETHZ-KPP-Kappa.png|248px|center]]
| |
| - |
| |
| - | == Analytical Solution ==
| |
| - | '''This completes the final equation describing the acetaldehyde gradient at steady state:'''
| |
| - | [[File:ETHZ-KPP-Final.png|684px|thumb|center|Analytical approximation of the acetaldehyde gradient]]
| |
| - |
| |
| - |
| |
| - | Finally, we also get an analytical expression for z<sub>DeadZone</sub>, at which both the acetaldehyde concentration and its gradient are zero:
| |
| - | [[File:ETHZ-KPP-zDeadZone.png|299px|center]]
| |
| - | {{:Team:ETH Zurich/Templates/SectionEnd}}
| |
| - |
| |
| - | {{:Team:ETH Zurich/Templates/SectionStart}}
| |
| - |
| |
| - | = GFP Band: Dimensionless Model =
| |
| - | == 1. Nondimensionalized System ==
| |
| - | We nondimensionalized all species occurring in the equations for the GFP band circuit.
| |
| - | [[File:ETHZ-Dimensionless-Species.png|140px|center]]
| |
| - | <br clear="all" />
| |
| - |
| |
| - | The dimensionless equations for the dynamics of the band-generating system then read
| |
| - | [[File:ETHZ-Dimensionless-Band.png|400px|center]]
| |
| - |
| |
| - | == 2. Steady State ==
| |
| - | [[File:ETHZ-Dimensionless-Band-SteadyState.png|412px|center]]
| |
| - |
| |
| - | == 3. Dimensionless Groupings ==
| |
| - | The equation system can be simplified by introducing the following dimensionless groupings:
| |
| - | [[File:ETHZ-Dimensionless-Groupings.png|179px|center]]
| |
| - |
| |
| - |
| |
| - | This yields the final equations for steady state:
| |
| - | [[File:ETHZ-Dimensionless-Band-SteadyState-Final.png|380px|center]]
| |
| - | {{:Team:ETH Zurich/Templates/SectionEnd}}
| |
| - |
| |
| - | {{:Team:ETH Zurich/Templates/SectionStart}}
| |
| - |
| |
| - | = GFP Band: Approximation & Analysis =
| |
| - | == 1. Splitting of Pathways ==
| |
| - | [[File:ETHZ-Analytical.png|600px|thumb|right]]
| |
| - | First, we split the band-pass system into both its long and short pathway:
| |
| - |
| |
| - | * Short pathway:
| |
| - | # AcAl
| |
| - | # TetR
| |
| - | # LacI<sub>M1</sub>
| |
| - | # GFP
| |
| - |
| |
| - | * Long pathway:
| |
| - | # AcAl
| |
| - | # TetR
| |
| - | # CI
| |
| - | # LacI
| |
| - | # GFP
| |
| - |
| |
| - |
| |
| - | <html><h3></html>Seperation of LacI Species<html></h3></html>
| |
| - | We separate the LacI species and their steady state equations in order to compute both pathways independently:
| |
| - |
| |
| - | [[File:ETHZ-Analytical-LacI.png|239px|center]]
| |
| - |
| |
| - | == 2. From GFP to Acetaldehyde ==
| |
| - | To get from GFP to Acetaldehyde, we have to invert all relevant equations:
| |
| - | {|align="center" width="100%"
| |
| - | |align="center"|'''Short pathway:'''
| |
| - | |align="center"|'''Long pathway:'''
| |
| - | |- valign="top"
| |
| - | |[[File:ETHZ-Analytical-ShortPath.png|center|216px]]
| |
| - | |[[File:ETHZ-Analytical-LongPath.png|center|216px]]
| |
| - | |}
| |
| - |
| |
| - | == 3. Half-Maximum GFP Activity ==
| |
| - | We first concentrate on the '''short pathway''' and determine for which acetaldehyde concentration it produces half-maximum GFP:
| |
| - | [[File:ETHZ-Analytical-GFPHalf-ShortPath.png|420px|center]]
| |
| - |
| |
| - | Next, we concentrate on the '''long pathway''':
| |
| - | [[File:ETHZ-Analytical-GFPHalf-LongPath.png|488px|center]]
| |
| - |
| |
| - |
| |
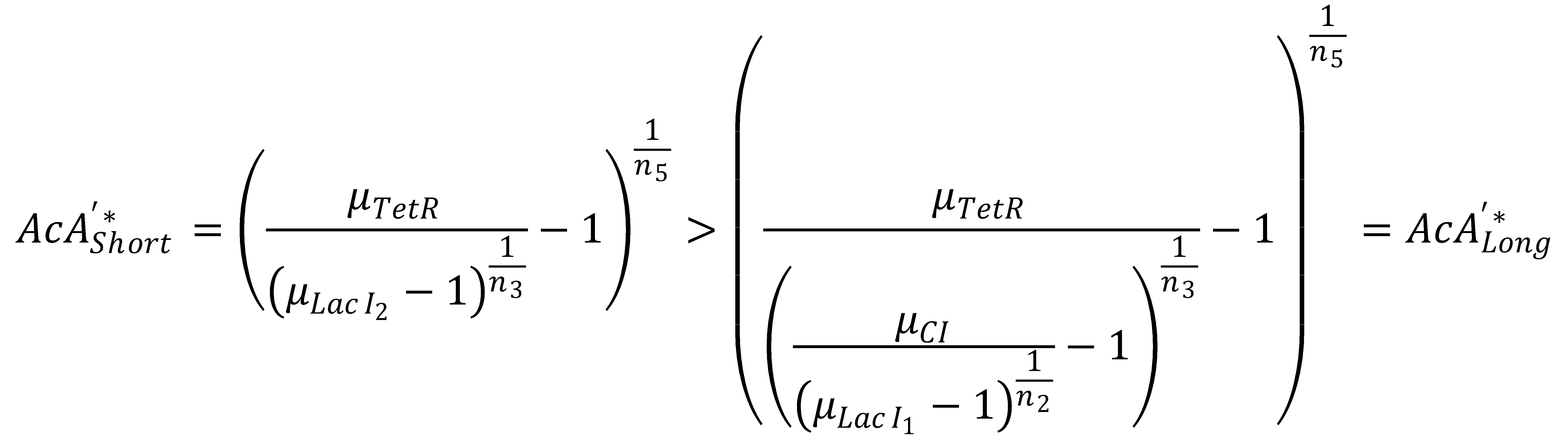
| | == 4. GFP Band Existence == | | == 4. GFP Band Existence == |
| | We can now derive a condition that has to be fulfilled in order for the GFP band to exist. Its meaning condenses down to the intuitive fact that the rising flank of the band has to occur "to the left" of the falling one. Mathematically, the condition can be derived from the following expression: | | We can now derive a condition that has to be fulfilled in order for the GFP band to exist. Its meaning condenses down to the intuitive fact that the rising flank of the band has to occur "to the left" of the falling one. Mathematically, the condition can be derived from the following expression: |
| Line 152: |
Line 10: |
| | | | |
| | <html><h3></html>Case Analysis<html></h3></html> | | <html><h3></html>Case Analysis<html></h3></html> |
| - | # Condition holds:
| + | * '''Condition holds:'''<br> This case is covered by our actual system implementation. In our system |
| - | # Corner Case (Equality):
| + | * Corner Case (Equality): |
| - | # Condition failure:
| + | * Condition failure: |
| | | | |
| | | | |
| | {{:Team:ETH Zurich/Templates/SectionEnd}} | | {{:Team:ETH Zurich/Templates/SectionEnd}} |
| | {{:Team:ETH Zurich/Templates/SectionStart}} | | {{:Team:ETH Zurich/Templates/SectionStart}} |
| - |
| |
| - | = References =
| |
| - | <span id="Ref1">[1]</span> [http://www.ncbi.nlm.nih.gov/pubmed/16209545 Valdés-Parada FJ, Alvarez-Ramírez J, Ochoa-Tapia JA.<br>'''An approximate solution for a transient two-phase stirred tank bioreactor with nonlinear kinetics.'''<br>Biotechnol Prog. 2005 Sep-Oct;21(5):1420-8.]
| |
| - | {{:Team:ETH Zurich/Templates/SectionEnd}}
| |
| - | {{:Team:ETH Zurich/Templates/HeaderNewEnd}}
| |
We can now derive a condition that has to be fulfilled in order for the GFP band to exist. Its meaning condenses down to the intuitive fact that the rising flank of the band has to occur "to the left" of the falling one. Mathematically, the condition can be derived from the following expression:
In Figure 1, this means that the dash-dotted red line must be at a lower acetaldehyde concentration than the blue dash-dotted red line. We now analyze what possible outcomes this condition has:
 "
"