Team:WHU-China/Project/Modeling

From 2011.igem.org

(Difference between revisions)
 
(95 intermediate revisions not shown)
Line 34: Line 34:
font-size:20px;
font-size:20px;
}
}
-
div.high
+
 
-
{
+
-
position:relative;
+
-
width:1000px;
+
-
top:30px;
+
-
height:1070px;
+
-
font-size:20px;
+
-
}
+
-
div.left
+
-
{
+
-
position:relative;
+
-
left:50px;
+
-
width:420px;
+
-
height:300px;
+
-
}
+
-
div.leftt
+
-
{
+
-
position:relative;
+
-
left:20px;
+
-
width:420px;
+
-
height:230px;
+
-
}
+
-
div.rightt
+
-
{
+
-
position:relative;
+
-
left:20px;
+
-
width:540px;
+
-
height:230px;
+
-
}
+
-
div.right
+
-
{
+
-
position:relative;
+
-
left:20px;
+
-
width:540px;
+
-
height:300px;
+
-
}
+
-
#left1
+
-
{
+
-
position:absolute;
+
-
width:420px;
+
-
left:0;
+
-
top:70px;
+
-
}
+
-
#right1
+
-
{
+
-
position:absolute;
+
-
width:580px;
+
-
left:420px;
+
-
}
+
-
#left2
+
-
{
+
-
position:absolute;
+
-
width:423px;
+
-
left:0;
+
-
top:100px;
+
-
}
+
-
#right2
+
-
{
+
-
position:absolute;
+
-
width:490px;
+
-
left:430px;
+
-
top:40px;
+
-
}
+
-
#intro
+
-
{
+
-
width:900px;
+
-
left:50px;
+
-
position:absolute;
+
-
}
+
</style>
</style>
Line 122: Line 54:
        
        
        
        
-
         if (Sys.chrome)       
+
         if (Sys.chrome||Sys.safari)       
  {
  {
-
   var a1=2880;
+
   var a1=2810;
   var a2=document.body.clientHeight;
   var a2=document.body.clientHeight;
   document.getElementById("bottom").style.top=(a2+a1).toString()+'px';
   document.getElementById("bottom").style.top=(a2+a1).toString()+'px';
Line 132: Line 64:
if(Sys.ie)
if(Sys.ie)
{
{
-
  var a1=2880;
+
  var a1=2780;
   var a2=document.body.clientHeight;
   var a2=document.body.clientHeight;
   document.getElementById("bottom").style.top=(a2+a1).toString()+'px';
   document.getElementById("bottom").style.top=(a2+a1).toString()+'px';
   document.getElementById("contact").style.top=(a2+a1+80).toString()+'px';
   document.getElementById("contact").style.top=(a2+a1+80).toString()+'px';
}else{
}else{
-
   var a1=2850;
+
   var a1=2780;
   var a2=document.body.clientHeight;
   var a2=document.body.clientHeight;
   document.getElementById("bottom").style.top=(a2+a1).toString()+'px';
   document.getElementById("bottom").style.top=(a2+a1).toString()+'px';
Line 148: Line 80:
<div id="content1">
<div id="content1">
<div  class="wide" id="wide1">
<div  class="wide" id="wide1">
-
In the mathematic modeling section , we make stimulation about the oscillator and consider two possible circumstance.
+
<div style="font-size:30px;font-family: 'Bodoni MT', Helvetica, sans-serif;" >Gene Circuit </div>
-
 
+
<img src="/wiki/images/c/cd/Oscillator5.png" width="80%" style="margin-left:10%"/>
-
</div>
+
-
 
+
-
<div class="high" id="high1">
+
-
<div id="left1" >
+
-
<div class="left" id="l1" style="left:60px;width:400px;height:130px">
+
-
The system including two protein:</br>
+
-
Using differential equation to describe the system:</br>
+
-
</div>
+
-
<div class="left" id="l2">
+
-
<p style="width:900px;">Where<img src="/wiki/images/e/ec/Image002.png"/>means the volume of<img src="/wiki/images/2/22/Image003.png" />,<img src="/wiki/images/8/89/Image004.png"/>means the volume of<img src="/wiki/images/3/3c/Image005.png" />,<img src="/wiki/images/3/3e/Image006.png" />means the delay time of the reaction.</p>
+
-
<p>&nbsp;&nbsp;&nbsp;&nbsp;This is the classic delay ODE , using the matlab software, we got the solution image ;</p>
+
-
</div>
+
-
<div class="left" id="l3">
+
-
<p style="width:600px">
+
-
We mainly consider the system including three protein:
+
-
We also use delay ODE to describe the system:</p>
+
-
</div>
+
-
<div class="left" id="l4">
+
-
 
+
-
<p style="position:absolute;top:-80px;">where:<img src="/wiki/images/0/06/Image010.png">means the volume of <img src="/wiki/images/7/79/Image011.png"></br> 
+
-
though dimensionless:</p>
+
<p>
<p>
-
The balance point of the equation is<img src="https://static.igem.org/mediawiki/2011/9/9e/Image013.png">and <img src="/wiki/images/1/1d/Image014.png"> </p>  
+
&nbsp;&nbsp;This is our gene circuit designed to equip our E.coli with the ability to change color with time.</br>  
-
</div>
+
&nbsp;&nbsp;The key players are LsrR and LsrK. The alternation of their expression results in the oscillating concentration of the reporter—GFP, and thus yield the periodically changing color. </br>
 +
&nbsp;&nbsp;Theoretically, at the very beginning, LsrR is expressed and inhibits LsrK. After some time, LsrR inhibits itself and its concentration drops. Therefore LsrK has a chance to express and climbs due to its self enlarging. However, LsrK induces the reexpression of LsrR at the same time. In this way, their concentrations wave alternatively. C1’s function is to delay the oscillation and stabilize the system.
 +
</p>
</div>
</div>
-
 
-
<div id="right1">
 
-
<div class="right" id="r1" style="height:190px;">
 
-
<img src="/wiki/images/7/79/Whu-m1.png" height="180" width="500">
 
-
</div>
 
-
<div class="right" id="r2">
 
-
<img src="/wiki/images/4/47/Whu-m2.png" height="200" width="350" style="position:absolute;top:50px;left:50px;">
 
-
</div>
 
-
<div class="right" id="r3">
 
-
<img src="/wiki/images/8/8e/Whu-m3.png" height="300" width="320" style="position:absolute;top:70px;left:-50px;>
 
-
</div>
 
-
<div class="right" id="r4" style="left:60px;">
 
-
 
-
</div>
 
-
</div>
 
-
 
-
 
-
</div>
 
-
 
-
 
<div class="wide" id="wide2">
<div class="wide" id="wide2">
-
<p style="position:relative;" >Using the MATLAB software to plot we got the solution image:</p>
+
<p></br></p>
-
<img src="/wiki/images/c/cc/Whu-m5.png" height="263" width="600" style="position:relative;left:150px;top:-10px;">
+
<div style="font-size:30px;font-family: 'Bodoni MT', Helvetica, sans-serif;">Modeling</div>
-
</div>
+
-
 
+
-
<div class="high" id="high2" style="height:950px;">
+
-
<div id="intro">
+
-
Bifurcation analysis chart:
+
-
</div>
+
-
<div id="left2">
+
-
<div class="leftt" id="l12">
+
-
 
+
<p>
<p>
-
<img src="/wiki/images/b/b2/Image017.png">is the Hopf bifurcation point, when<img src="/wiki/images/d/d3/Image018.png">,it is able to generate a stable periodic solution.</p>
+
&nbsp;&nbsp;In the part of waving time, there is a two nodes system .Using the method of the mathematic theory of the ODE and the stochastic process.,we get our models.In the models, X1 denotes LsrK, X2 denotes LsrR.</br>
-
</div>
+
&nbsp;&nbsp;First we generate a ODE to describe the system:
-
<div class="leftt" id="l22">
+
</p>
-
 
+
<img src="/wiki/images/c/c3/Model-1.png" style="margin-left:2%"/>
<p>
<p>
-
<img src="/wiki/images/7/71/Image020.png">is the Hopf bifurcation point, when<img src="/wiki/images/f/f1/Image021.png">,it is able to generate a stable periodic solution.</p>
+
&nbsp;&nbsp;the solution diagram of the function is:
-
</div>
+
</p>
-
<div class="leftt" id="l32">
+
<img src="/wiki/images/e/e3/Model-2.png" style="margin-left:2%"/>
-
 
+
<p>
 +
&nbsp;&nbsp;Taking the fluctuations arising from the molecules into account, we need to resort to stochastic simulations. We use here the Gillespie algorithm to simulate a stochastic version of the model.Suppose the system size Ω=1000,then we can get the result of simulation.
 +
</p>
 +
<img src="/wiki/images/0/04/Model-3.png" style="margin-left:2%"/>
<p>
<p>
-
<img src="/wiki/images/8/81/Image023.png">is the Hopf bifurcation point, when<img src="/wiki/images/0/0d/Image024.png">,it is able to generate a stable periodic solution.</p>
+
&nbsp;&nbsp;Bifurcation diagram:
 +
</p>
 +
<img src="/wiki/images/7/77/Model-a1-b2-1.png" width="80%" style="margin-left:2%"/>
 +
<p>
 +
&nbsp;&nbsp;Period evolution with parameters：
 +
</p>
 +
<img src="/wiki/images/2/22/Model-a1-b2-2.png" width="80%" style="margin-left:2%"/>
 +
<p>
 +
&nbsp;&nbsp;Due to the conclusion we can find that the b1 is more sensitive to the period. If we want to change the period of the system , it more efficient to adjust the parameter of b2 and then adjust the biological properties.  
 +
</p>
</div>
</div>
-
<div class="leftt" id="l42">
 
 +
<div class="wide" id="wide3">
 +
<p></br></p>
 +
<div style="font-size:30px;font-family: 'Bodoni MT', Helvetica, sans-serif;">Conclusion</div>
<p>
<p>
-
<img src="/wiki/images/8/8d/Image026.png">is the Hopf bifurcation point, when<img src="/wiki/images/9/94/Image027.png">,it is able to generate a stable periodic solution.</p>
+
&nbsp;&nbsp;As the changes of period with the change of the parameters in the image , we can get the conclusion that: </br>
-
</div>
+
1. &nbsp;&nbsp;&nbsp;&nbsp;a1,a2,a3,b1  has a little influence on period. </br>
-
</div>
+
2. &nbsp;&nbsp;&nbsp;&nbsp;b2 has inversely proportional relationship with period , it has a huge influence on the period. </br>
 +
&nbsp;&nbsp;This conclusion we get before can be used to guide the design of biological systems. In order to achieve the adjustment of &nbsp;&nbsp;period, we can adjust the size of some parameters.</br>
 +
Both the deterministic and stochastic models confirm our conjecture that the oscillator can work stably.
-
<div id="right2">
+
</p>
-
<div class="rightt" id="r12">
+
-
<img src="/wiki/images/8/89/Whu-m6.png" height="220" width="450">
+
</div>
</div>
-
<div class="rightt" id="r22">
+
<div style="height:100px"></div>
-
<img src="/wiki/images/c/c9/Whu-m7.png" height="220" width="450">
+
-
</div>
+
-
<div class="rightt" id="r32">
+
-
<img src="/wiki/images/0/0f/Whu-m8.png" height="220" width="450">
+
-
</div>
+
-
<div class="rightt" id="r42">
+
-
<img src="/wiki/images/4/49/P9.png" height="220" width="450">
+
-
</div>
+
-
</div>
+
-
 
+
-
</div>
+
-
 
+
-
<div class="wide" id="wide3" >
+
-
<p>Cycle with the curve of each parameter:</p>
+
-
<img src="/wiki/images/0/0a/Whu-m10.png" height="350" width="600" style="position:relative;left:100px;"/>
+
-
 
+
-
 
+
-
 
+
-
 
+
-
<div style="position:relative">
+
-
<p>As the changes of cycle time with the change of the parameters in the image , we can get the conclusion that:</br>
+
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;1.<img src="/wiki/images/0/04/Image029.png"/>have little influence on the range.</br>
+
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;2.<img src="/wiki/images/8/82/Image030.png"/>do not have much influence on the cycle time.</br>
+
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;3.<img src="/wiki/images/1/11/Image031.png"/>have inversely proportional relationship with the cycle time , it have a huge influence on the cycle &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;time , but little impact on the range (Can be used to adjust the cycle to maintain constant amplitude)</br>
+
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;4.When<img src="/wiki/images/9/94/Image032.png"/>,<img src="/wiki/images/2/21/Image033.png"/> have little influence on the range.
+
-
</br>
+
-
This conclusion we get before can be used to guide the design of biological systems, in order to achieve the adjustment period, amplitude can adjust the size of some parameters.</p></div>
+
-
 
+
-
</div>
+
-
 
+
-
 
+
-
<div style="height:100px;"></div>
+
-
 
+
-
 
+
<div id="bottom">
<div id="bottom">
<image src="/wiki/images/5/58/Whu-backgroundbottom.png"/>
<image src="/wiki/images/5/58/Whu-backgroundbottom.png"/>

Latest revision as of 03:33, 29 October 2011

Gene Circuit

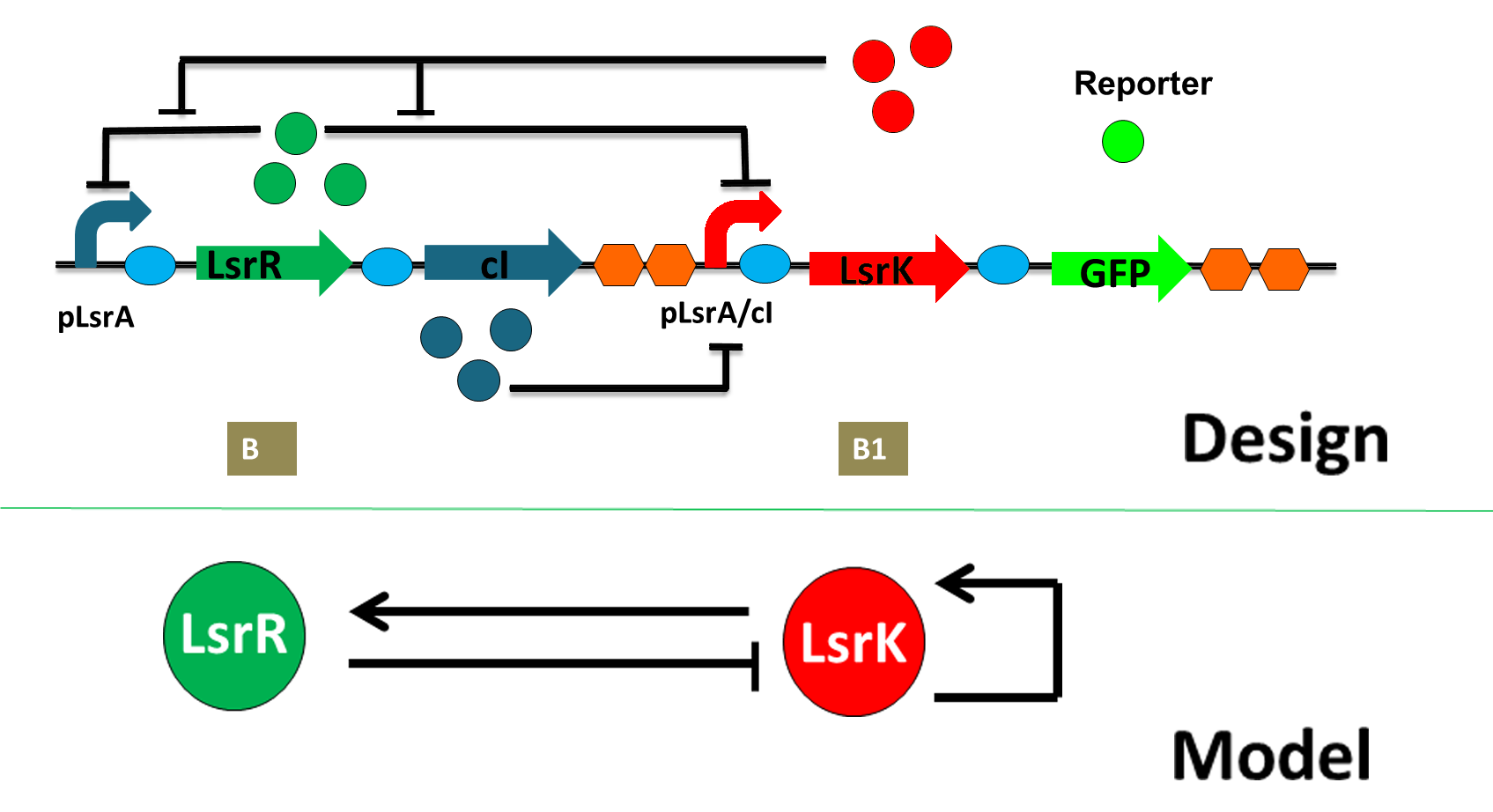
  This is our gene circuit designed to equip our E.coli with the ability to change color with time.
  The key players are LsrR and LsrK. The alternation of their expression results in the oscillating concentration of the reporter—GFP, and thus yield the periodically changing color.
  Theoretically, at the very beginning, LsrR is expressed and inhibits LsrK. After some time, LsrR inhibits itself and its concentration drops. Therefore LsrK has a chance to express and climbs due to its self enlarging. However, LsrK induces the reexpression of LsrR at the same time. In this way, their concentrations wave alternatively. C1’s function is to delay the oscillation and stabilize the system.


Modeling

  In the part of waving time, there is a two nodes system .Using the method of the mathematic theory of the ODE and the stochastic process.,we get our models.In the models, X1 denotes LsrK, X2 denotes LsrR.
  First we generate a ODE to describe the system:

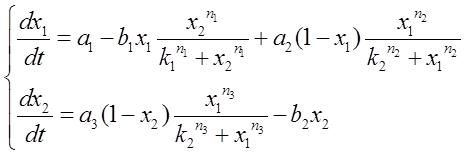
  the solution diagram of the function is:

  Taking the fluctuations arising from the molecules into account, we need to resort to stochastic simulations. We use here the Gillespie algorithm to simulate a stochastic version of the model.Suppose the system size Ω=1000,then we can get the result of simulation.

  Bifurcation diagram:

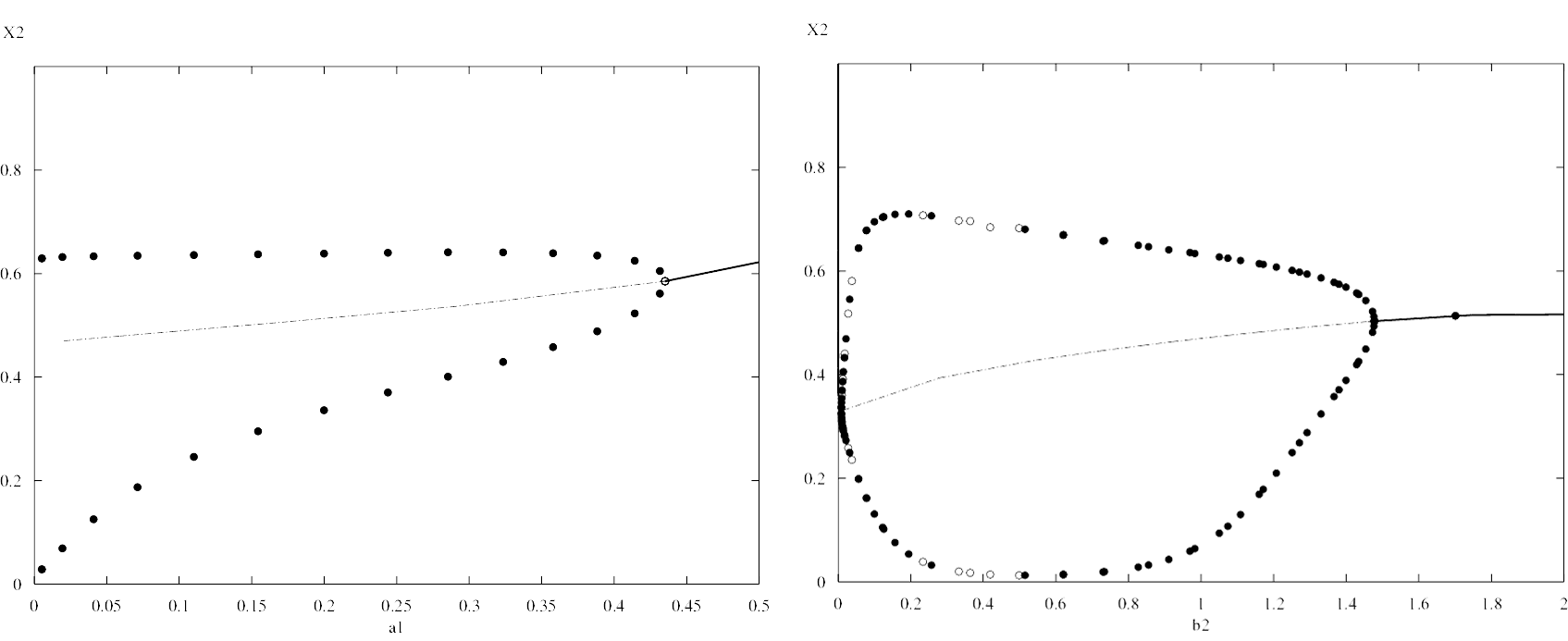
  Period evolution with parameters：

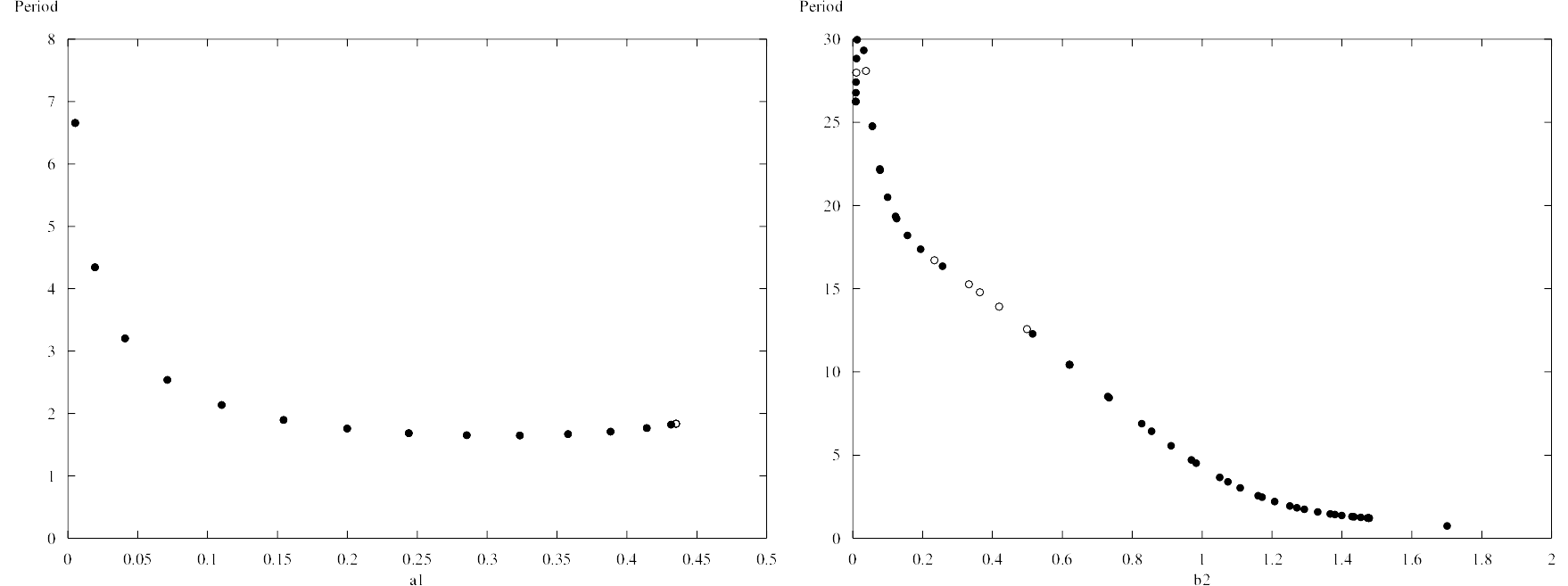
  Due to the conclusion we can find that the b1 is more sensitive to the period. If we want to change the period of the system , it more efficient to adjust the parameter of b2 and then adjust the biological properties.


Conclusion

  As the changes of period with the change of the parameters in the image , we can get the conclusion that:
1.     a1,a2,a3,b1 has a little influence on period.
2.     b2 has inversely proportional relationship with period , it has a huge influence on the period.
  This conclusion we get before can be used to guide the design of biological systems. In order to achieve the adjustment of   period, we can adjust the size of some parameters.
Both the deterministic and stochastic models confirm our conjecture that the oscillator can work stably.

Count Down

days

hours

minutes

seconds

Visitor

Retrieved from "http://2011.igem.org/Team:WHU-China/Project/Modeling"